题目内容
(2007•汕头二模)中央电视台《福州月SKIPIF 1<0中华情》大型中秋晚会今年在我市海峡会展中心举行,之前甲、乙两人参加大会青年志愿者的选拔.已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选.
(1)求甲答对试题数ξ的概率分布及数学期望;
(2)求甲、乙两人至少有一人入选的概率.
(1)求甲答对试题数ξ的概率分布及数学期望;
(2)求甲、乙两人至少有一人入选的概率.
分析:(1)甲答对试题数的可能取值为0,1,2,3,结合变量对应的事件和等可能事件的概率公式,得到变量的概率,写出分布列.做出期望值.
(2)先求甲、乙两人考试合格的事件的概率,从而可求甲、乙两人考试均不合格的概率,进而用对立事件,可求甲、乙两人至少一个合格的概率.
(2)先求甲、乙两人考试合格的事件的概率,从而可求甲、乙两人考试均不合格的概率,进而用对立事件,可求甲、乙两人至少一个合格的概率.
解答:解:(1)甲答对试题数ξ的可能取值为0,1,2,3,
p(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
.
∴ξ的分布列如下:
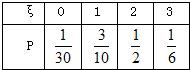
∴Eξ=0×
+1×
+2×
+3×
=
.
(2)设甲、乙两人考试合格的事件分别为A、B
则 P(A)=
=
,
P(B)=
=
,
甲、乙两人考试均不合格的概率为:P(
)=P(
)•P(
)=(1-
)(1-
)=
×
=
,
∴甲、乙两人至少一个合格的概率为P=1-P(
)=1-
=
.
p(ξ=0)=
| ||
|
| 1 |
| 30 |
P(ξ=1)=
| ||||
|
| 3 |
| 10 |
P(ξ=2)=
| ||||
|
| 1 |
| 2 |
P(ξ=3)=
| ||
|
| 1 |
| 6 |
∴ξ的分布列如下:

∴Eξ=0×
| 1 |
| 30 |
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 6 |
| 9 |
| 5 |
(2)设甲、乙两人考试合格的事件分别为A、B
则 P(A)=
| ||||||
|
| 2 |
| 3 |
P(B)=
| ||||||
|
| 14 |
| 15 |
甲、乙两人考试均不合格的概率为:P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 2 |
| 3 |
| 14 |
| 15 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 45 |
∴甲、乙两人至少一个合格的概率为P=1-P(
. |
| A |
. |
| B |
| 1 |
| 45 |
| 44 |
| 45 |
点评:本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,考查利用概率知识解决实际问题的能力,是一个比较好的概率解答题.

练习册系列答案
相关题目
 (2007•汕头二模)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )
(2007•汕头二模)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过70km/h的汽车数量为( ) (2007•汕头二模)如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(精确到0.1km).
(2007•汕头二模)如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(精确到0.1km).