题目内容
定义:关于x的两个不等式f(x)<0和g(x)<0的解集分别为(a,b)和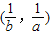 ,则称这两个不等式为对偶不等式.如果不等式
,则称这两个不等式为对偶不等式.如果不等式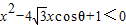 与不等式x2+12xsinθ+1<0为对偶不等式,且
与不等式x2+12xsinθ+1<0为对偶不等式,且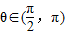 ,则θ= .
,则θ= .
【答案】分析:先设出不等式x2-4 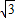 xcosθ+1<0的对应方程两个根为a、b,推出不等式x2-4
xcosθ+1<0的对应方程两个根为a、b,推出不等式x2-4 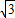 xcosθ+1<0的对应方程两个根为a、b,利用韦达定理,求得关于θ的三角方程,根据θ的范围求解即可.
xcosθ+1<0的对应方程两个根为a、b,利用韦达定理,求得关于θ的三角方程,根据θ的范围求解即可.
解答:解:设不等式x2-4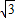 xcosθ+1<0的解集为(a,b),由题意可得不等式x2+12xsinθ+1<0的解集
xcosθ+1<0的解集为(a,b),由题意可得不等式x2+12xsinθ+1<0的解集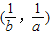 ,
,
由一元二次方程与不等式的关系可知,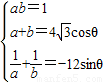
整理可得,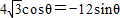
∴tanθ=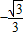 ,且θ∈(
,且θ∈( 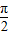 ,π),
,π),
∴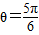
故答案为: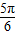
点评:本题主要考查了一元二次不等式的应用,以及根与系数的关系和韦达定理,同时考查了解三角方程,属于中档题.
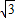 xcosθ+1<0的对应方程两个根为a、b,推出不等式x2-4
xcosθ+1<0的对应方程两个根为a、b,推出不等式x2-4 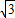 xcosθ+1<0的对应方程两个根为a、b,利用韦达定理,求得关于θ的三角方程,根据θ的范围求解即可.
xcosθ+1<0的对应方程两个根为a、b,利用韦达定理,求得关于θ的三角方程,根据θ的范围求解即可.解答:解:设不等式x2-4
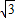 xcosθ+1<0的解集为(a,b),由题意可得不等式x2+12xsinθ+1<0的解集
xcosθ+1<0的解集为(a,b),由题意可得不等式x2+12xsinθ+1<0的解集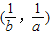 ,
,由一元二次方程与不等式的关系可知,
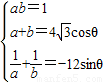
整理可得,
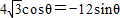
∴tanθ=
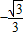 ,且θ∈(
,且θ∈( 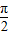 ,π),
,π),∴
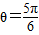
故答案为:
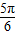
点评:本题主要考查了一元二次不等式的应用,以及根与系数的关系和韦达定理,同时考查了解三角方程,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
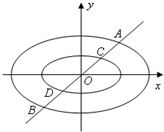 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 (2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
(2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆