题目内容
已知△ABC中,∠ABC=90°,P为△ABC所在平面外一点,PA=PB=PC.求证:平面PAC⊥平面ABC.
证明:取AC的中点为O,连结OP、OB,
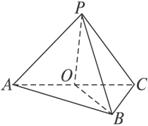
∵AO=OC,PA=PC,∴PO⊥AC.
∵∠ABC=90°,
∴OB=OA.
又PB=PA,PO=PO,
∴△POB≌△POA.
∴PO⊥OB.
∴PO⊥平面ABC.
∴平面PAC⊥平面ABC.
小结:本例的证明过程主要是证PO⊥平面ABC.
练习册系列答案
金钥匙试卷系列答案
相关题目
金钥匙试卷系列答案
,b=1,B=30°,则其面积等于( )
或
B.
C.
或
D.
的坐标.