Question

有下列五个命题：
①{a_n}为等比数列，S_n是其前n项和，则S₄，S₈-S₄，S₁₂-S₈成等比数列；
②在同一坐标系中，当x∈（-

π

2

，

π

2

）时，y=sinx与y=tanx的图象有且只有一个交点；
③在一个四面体中，四个面有可能全是直角三角形；
④f（x）=x²-2x+5，x∈（-∞，1），则f^-1（x）=1+

x-4

，x∈（4，+∞）；
⑤当m²+

1

n(m-n)

的最小值为4．
其中直命题是

 

（填出所有真命题的编号）．

Answer 1

分析：对于①由于{a_n}为等比数列，S_n是其前n项和，若S_n=0，则可以加以判断；
对于②由题意画出在同一坐标系中，当x∈（-

π

2

，

π

2

）时，画出y=sinx与y=tanx的图象即可判断；
对于③在一个四面体中，四个面有可能全是直角三角形，通过画出实际图形加以判断；
对于④f（x）=x²-2x+5利用反函数的定义求出反函数即可；
对于⑤m²+

1

n(m-n)

利用均值不等式即可判断．

解答：解：①因为{a_n}为等比数列，S_n是其前n项和，在若S₄，S₈-S₄，S₁₂-S₈求和为0时，则就不成等比数列；
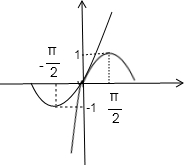
②由题意画出图象为：易有当x∈（-

π

2

，

π

2

）时，y=sinx与y=tanx的图象交点只有一个为（0，0），所以②正确；

③有空间想象出图象为：

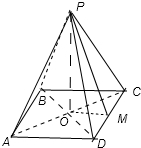
在正四棱锥中，点M为边CD的中点，则四棱锥P-ODM即为四个面全为直角三角形的四棱锥，所以③正确；
④由于函数f（x）=x²-2x+5，x∈（-∞，1），所以值域为（4，+∞），令y=x²-2x+5=（x-1）²+4
?f-1(x)=1+

x-4

 （4，+∞），所以④正确；
⑤令y=m²+

1

n(m-n)

由于m，n的大小及正负都不知，有均值不等式的条件可以知道⑤错．
故答案为：②③④

点评：此题考查了反函数的定义及求一个函数的反函数，还考查了学生的空间想象能力，及正弦函数与正切函数的图象，还考查了均值不等式．