题目内容
设 的取值范围是
的取值范围是
- A.[2,+∞)
- B.

- C.
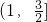
- D.
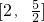
C
分析:将a+b=ab-3代入 ,从而确定a+b的范围,可求
,从而确定a+b的范围,可求 的取值范围.
的取值范围.
解答:将a+b=ab-3代入
∵a>0,b>0,
∴
∴
∵ab=a+b+3
∴
∴(a+b)2-4(a+b)-12≥0
∴a+b≥6或a+b≤-2
∵a>0,b>0
∴a+b≥6
∴
∴
∴ 的取值范围是
的取值范围是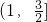
故选C.
点评:本题以等式为载体,考查代数式的范围,解题的关键是等式的变形与利用基本不等式.
分析:将a+b=ab-3代入
 ,从而确定a+b的范围,可求
,从而确定a+b的范围,可求 的取值范围.
的取值范围.解答:将a+b=ab-3代入

∵a>0,b>0,
∴

∴

∵ab=a+b+3
∴

∴(a+b)2-4(a+b)-12≥0
∴a+b≥6或a+b≤-2
∵a>0,b>0
∴a+b≥6
∴

∴

∴
 的取值范围是
的取值范围是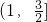
故选C.
点评:本题以等式为载体,考查代数式的范围,解题的关键是等式的变形与利用基本不等式.

练习册系列答案
相关题目
 动点P在以点C为圆心且与直线BD相切的圆内运动,设
动点P在以点C为圆心且与直线BD相切的圆内运动,设 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.
 动点P在以点C为圆心
动点P在以点C为圆心 且与直线BD相切的圆内运动,设
且与直线BD相切的圆内运动,设 的
的 取值范围是
取值范围是



