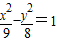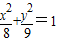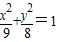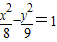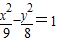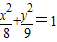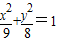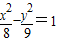题目内容
已知圆O′：（x-1）2+y2=36，点A（-1，0），M是圆上任意一点，线段AM的中垂线l和直线O′M相交于点Q，则点Q的轨迹方程为（ ）
分析：由题意画出图形，通过把Q到A和O′的距离转化得到Q点的轨迹为椭圆，然后直接由椭圆定义得方程．
解答：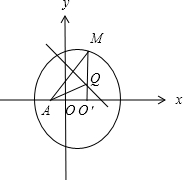
解：如图，联结QA，由于Q在AM的中垂线上，有|QA|=|QM|，
则|QA|+|QO′|=|QM|+|QO′|=|O′M|．
O′M是⊙O′的半径，|O′M|=6．
所以Q到A、O′的距离之和为定值，轨迹为椭圆
椭圆的焦点是A、O′，中心是AO′中点
由于A（-1，0），O′（1，0），
所以c=1，a=3．
则b2=a2-c2=8．
则椭圆的方程是：
+
=1．
即Q的轨迹方程为
+
=1．
故选C．
解：如图，联结QA，由于Q在AM的中垂线上，有|QA|=|QM|，则|QA|+|QO′|=|QM|+|QO′|=|O′M|．
O′M是⊙O′的半径，|O′M|=6．
所以Q到A、O′的距离之和为定值，轨迹为椭圆
椭圆的焦点是A、O′，中心是AO′中点
由于A（-1，0），O′（1，0），
所以c=1，a=3．
则b2=a2-c2=8．
则椭圆的方程是：
| x2 |
| 9 |
| y2 |
| 8 |
即Q的轨迹方程为
| x2 |
| 9 |
| y2 |
| 8 |
故选C．
点评：本题考查了与直线有关的动点轨迹方程，考查了椭圆的定义，利用线段垂直平分线上的点到线段两端点的距离相等是解答该题的关键，是中档题．
练习册系列答案
相关题目
