Question

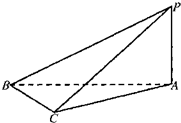
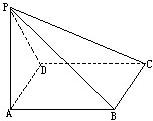
如图，在三棱锥P-ABC中，∠PAB=∠PAC=∠ACB=90°．
（1）求证：平面PBC丄平面PAC
（2）已知PA=1，AB=2，当三棱锥P-ABC的体积最大时，求BC的长．

Answer 1

（1）证明：∵∠PAB=∠PAC=90°，∴PA⊥AB，PA⊥AC，
∵AB∩AC=A，∴PA⊥平面ABC，
∵BC?平面ABC，∴BC⊥PA
∵∠ACB=90°，∴BC⊥CA，又PA∩CA=A，
∴BC⊥平面PAC，∵BC?平面PBC，
∴平面PBC⊥平面PAC．
（2）由（1）知：PA⊥平面ABC，BC⊥CA，
设BC=x（0＜x＜2），AC=

AB2-BC2

=

22-x2

=

4-x2

，
V_P-ABC=

1

3

×S_△ABC×PA=

1

6

x

4-x2

=

1

6

x2(4-x2)

≤

1

6

×

x2+4-x2

2

=

1

3

．
当且仅当x=

2

时，取“=”，
故三棱锥P-ABC的体积最大为

1

3

，此时BC=

2

．