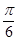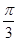题目内容
定义域为 的函数
的函数 (
( )有两个单调区间,则实数
)有两个单调区间,则实数 ,
, ,
, 满足( )
满足( )
A. 且 且 | B. | C. | D. |
(D)
解析试题分析:由于函数 (
( )有两个单调区间.函数
)有两个单调区间.函数 为偶函数.当
为偶函数.当 时,函数
时,函数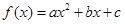 .对称轴
.对称轴 ,保证函数在
,保证函数在 时只有单调递增或单调递减,函数
时只有单调递增或单调递减,函数 有两个单调区间.故选(D).
有两个单调区间.故选(D).
考点:1.函数的单调性.2.函数的奇偶性.3.归纳化归的思想.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知函数 在
在 上的最大值为
上的最大值为 ,则函数
,则函数
的零点的个数为( )
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
函数 在定义域内零点的个数为( )
在定义域内零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知偶函数 满足
满足 ,且当
,且当 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上根的个数是( )
上根的个数是( )
A. 个 个 | B. 个 个 | C. 个 个 | D. |
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)=( )
| A.-1 | B.1 | C.-2 | D.2 |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.[1,+∞) |
| C.(0,1] | D.(0,1) |
下列函数中,函数图象关于y轴对称,且在(0,+∞)上单调递增的是( )
| A.y=2x | B.y=x2﹣1 | C.y= | D.y= |



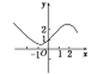
 (
( )的图象绕坐标原点逆时针旋转
)的图象绕坐标原点逆时针旋转 (
(