题目内容
设函数ω(其中A>0,ω>0,-π<φ<π )在x= 处取得最大值2,其图象与轴的相邻两个交点的距离为
处取得最大值2,其图象与轴的相邻两个交点的距离为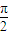 .
.(I)求f(x)的解析式;
(II)求函数f(x)的值域.
【答案】分析:(I)通过函数的周期求出ω,求出A,利用函数经过的特殊点求出φ,推出f(x)的解析式;
(II)直接利用函数的解析式,通过正弦函数的值域求出所求函数的值域即可.
解答:解:(Ⅰ)由题意可知f(x)的周期为T=π,即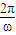 =π,解得ω=2.
=π,解得ω=2.
因此f(x)在x= 处取得最大值2,所以A=2,从而sin(2×
处取得最大值2,所以A=2,从而sin(2×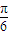 +φ)=1,
+φ)=1,
所以 +φ=
+φ= +2kπ,k∈z,又-π<φ≤π,得φ=
+2kπ,k∈z,又-π<φ≤π,得φ= ,
,
故f(x)的解析式为f(x)=2sin(2x+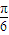 );
);
(Ⅱ)因为y=sinx∈[-1,1],
所以sin(2x+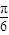 )∈[-1,1];则2sin(2x+
)∈[-1,1];则2sin(2x+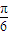 )∈[-2,2];
)∈[-2,2];
函数f(x)的值域:[-2,2]
点评:本题考查三角函数的解析式的求法,正弦函数的值域的应用,考查计算能力.
(II)直接利用函数的解析式,通过正弦函数的值域求出所求函数的值域即可.
解答:解:(Ⅰ)由题意可知f(x)的周期为T=π,即
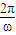 =π,解得ω=2.
=π,解得ω=2.因此f(x)在x=
 处取得最大值2,所以A=2,从而sin(2×
处取得最大值2,所以A=2,从而sin(2×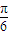 +φ)=1,
+φ)=1,所以
 +φ=
+φ= +2kπ,k∈z,又-π<φ≤π,得φ=
+2kπ,k∈z,又-π<φ≤π,得φ= ,
,故f(x)的解析式为f(x)=2sin(2x+
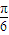 );
);(Ⅱ)因为y=sinx∈[-1,1],
所以sin(2x+
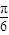 )∈[-1,1];则2sin(2x+
)∈[-1,1];则2sin(2x+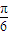 )∈[-2,2];
)∈[-2,2];函数f(x)的值域:[-2,2]
点评:本题考查三角函数的解析式的求法,正弦函数的值域的应用,考查计算能力.

练习册系列答案
相关题目
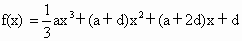 ,
,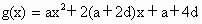 ,其中a>0,d>0,设
,其中a>0,d>0,设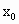 为f(x)的极小值点,
为f(x)的极小值点,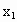 为g(x)的极值点,
为g(x)的极值点,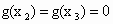 ,并且
,并且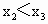 ,将点(
,将点(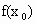 ),(
),(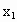 ,
,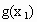 ),(
),(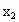 ,0),(
,0),(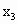 ,0)依次记为A,B,C,D.
,0)依次记为A,B,C,D.