题目内容
(本题满分14分
已知椭圆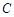 :
: 的离心率为
的离心率为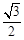 ,以原点为圆心,
,以原点为圆心,
椭圆的短半轴长为半径的圆与直线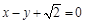 相切.
相切.
⑴求椭圆C的方程;
⑵设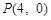 ,
, 、
、 是椭圆
是椭圆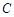 上关于
上关于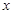 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结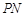 交椭圆
交椭圆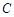
于另一点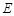 ,求直线
,求直线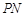 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线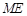 与
与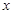 轴相交于定点.
轴相交于定点.
【答案】
⑴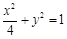 ;
;
⑵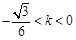 或
或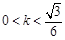 ;
;
⑶见解析
【解析】本题考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是确定几何量之间的关系,利用直线与椭圆联立,结合韦达定理求解
(1)根据椭圆的性质,离心率得到参数a,c的关系,然后利用线与圆相切得到参数b的值,进而得到椭圆的方程。
(2)设出直线与椭圆的方程联立方程组,结合韦达定理,和判别式大于零得到直线的斜率的范围。
(3)表示直线ME的方程,以及结合点的坐标的对称关系,得到k的关系式,进而得到直线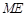 与
与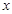 轴相交于定点
轴相交于定点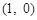
解:⑴由题意知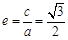 ,
,
所以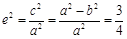 ,即
,即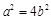 ,
,
又因为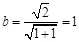 ,所以
,所以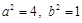 ,
,
故椭圆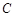 的方程为
的方程为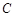 :
: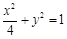 .-----------4分
.-----------4分
⑵由题意知直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为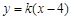 ①
①
联立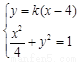 消去
消去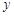 得:
得: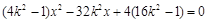 ,
,
由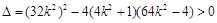 得
得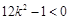 ,
,
又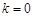 不合题意,
不合题意,
所以直线 的斜率的取值范围是
的斜率的取值范围是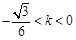 或
或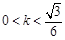 .---8分
.---8分
⑶设点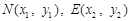 ,则
,则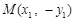 ,
,
直线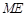 的方程为
的方程为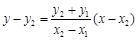 ,
,
令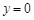 ,得
,得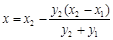 ,
,
将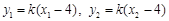 代入整理,得
代入整理,得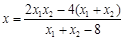 . ②
. ②
由得①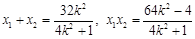 代入②整理,得
代入②整理,得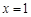 ,
,
所以直线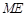 与
与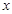 轴相交于定点
轴相交于定点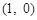 . ----------------14分
. ----------------14分

练习册系列答案
相关题目
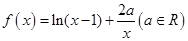
 的单调区间;
的单调区间;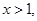 且
且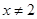 时,
时,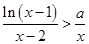 恒成立,求实数
恒成立,求实数 的范围.
的范围.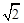 .M为线段PC的中点.
.M为线段PC的中点.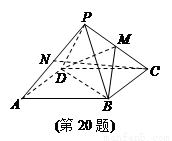
 的图像过点(1,3),且
的图像过点(1,3),且 对任意实数都成立,函数
对任意实数都成立,函数 与
与 的图像关于原点对称.
的图像关于原点对称. 与
与 的解析式;
的解析式; 在[-1,1]上是增函数,求实数λ的取值范围.
在[-1,1]上是增函数,求实数λ的取值范围.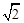 .M为线段PC的中点.
.M为线段PC的中点.