题目内容
7.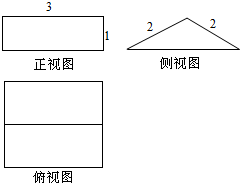 一个几何体的正视图是长为3、宽为1的矩形,侧视图是腰长为2的等腰三角形,则该几何的表面积为12+8$\sqrt{3}$.
一个几何体的正视图是长为3、宽为1的矩形,侧视图是腰长为2的等腰三角形,则该几何的表面积为12+8$\sqrt{3}$.
分析 根据几何体的三视图,得出该几何体是平放的直三棱柱,结合图中数据求出它的表面积.
解答 解:根据几何体的三视图,得;
该几何体是平放的直三棱柱,且三棱柱的侧棱长为3,
底面三角形为等腰三角形,等腰长为2,底边上的高为1;
∴底边长为2$\sqrt{{2}^{2}{-1}^{2}}$=2$\sqrt{3}$,
∴该三棱柱的表面积为
S=S底+S侧=2×$\frac{1}{2}$×2$\sqrt{3}$×1+(2+2+2$\sqrt{3}$)×3=12+8$\sqrt{3}$.
故答案为:12+8$\sqrt{3}$.
点评 本题考查了利用空间几何体的三视图求表面积的应用问题,是基础题目.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
17.若满足条件C=30°,AB=2,BC=a的△ABC有两个,那么a的取值范围是( )
| A. | (1,2) | B. | (1,2$\sqrt{3}$) | C. | (2,4) | D. | (2,4$\sqrt{3}$) |
18.若实数x,y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥2}\\{x≤1}\end{array}\right.$,则2x+y的最大值为( )
| A. | 5 | B. | 4 | C. | 3 | D. | $\frac{5}{2}$ |
17.设x,y满足y=-x+1,则x2+y2的最小值为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | 2 |
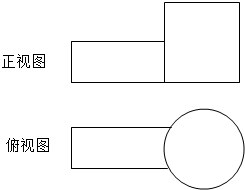 如图是某几何体的正视图和俯视图,试分析此几何体的结构特征,并画出其侧视图.
如图是某几何体的正视图和俯视图,试分析此几何体的结构特征,并画出其侧视图.