题目内容
设m是正实数．若椭圆
+
=1的焦距为8，则m= ．
| x2 |
| m2+16 |
| y2 |
| 9 |
分析：因为a2=m2+16，b2=9，所以c2=m2+16-9=m2+7，由此能得到焦距，列出关于m的方程求得m 值．
解答：解：∵a2=m2+16，b2=9，
∴c2=m2+16-9=m2+7，
∴2c=8，
∴
=4，⇒m=3
故答案为：3．
∴c2=m2+16-9=m2+7，
∴2c=8，
∴
| m 2+7 |
故答案为：3．
点评：本题考查椭圆的简单性质、椭圆的标准方程、方程的解法等基础知识，考查运算求解能力，考查数形结合思想，解题时要注意公式的灵活运用．
练习册系列答案
相关题目
（2012•河北模拟）如图，已知椭圆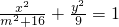
的焦距为8，则m=________．