题目内容
已知随机变量ξ的分布列为且η=2ξ+3，则Eη等于（ ）
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
分析：根据条件中所给的随机变量的分布列，可以写出变量的期望，对于Eη的结果，需要根据期望的公式E（ax+b）=aE（x）+b，代入前面做出的期望，得到结果．
解答：解：由条件中所给的随机变量的分布列可知
Eξ=0×
+1×
+2×
=
∵η=2ξ+3，E（2ξ+3）=2Eξ+3，
∴Eη=E（2ξ+3）=2×
+3=
．
故选C．
Eξ=0×
| 7 |
| 15 |
| 7 |
| 15 |
| 1 |
| 15 |
| 3 |
| 5 |
∵η=2ξ+3，E（2ξ+3）=2Eξ+3，
∴Eη=E（2ξ+3）=2×
| 3 |
| 5 |
| 21 |
| 5 |
故选C．
点评：本题考查离散型随机变量的分布列和期望，考查具有一定关系的变量之间的期望的关系，是一个基础题，是运算量很小的一个问题．
练习册系列答案
相关题目
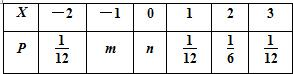已知随机变量X的分布列如图：其中m，n∈[0，1），且E（X）=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|