题目内容
已知函数
 .
.
(1)若 ,讨论函数
,讨论函数 在区间
在区间 上的单调性;
上的单调性;
(2)若 且对任意的
且对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(1) 时,
时, ,则
,则 ,
,
当 时,
时, ,所以函数
,所以函数 在区间
在区间 上单调递减
上单调递减
当 时,
时, ,所以函数
,所以函数 在区间
在区间 上单调递增;
上单调递增;
当 时,存在
时,存在 ,使得
,使得 ,即
,即 ,
,
 时,
时, ,函数
,函数 在区间
在区间 上单调递增
上单调递增
 时,
时, ,函数
,函数 在区间
在区间 上单调递减.
上单调递减.
(2) 时,
时, ,
,
 恒成立,等价于
恒成立,等价于 ,
,
记 ,
,
则 ,
,
当 ,即
,即 时,
时, ,
, 在区间
在区间 上单调递减,
上单调递减,
所以当 时,
时, ,即
,即 恒成立;
恒成立;
当 ,即
,即 时,记
时,记 ,则
,则 ,
,
存在 ,使得
,使得 ,
,
此时 时,
时, ,
, 单调递增,
单调递增, ,即
,即 ,
,
所以 ,即
,即 ,不合题意;
,不合题意;
当 时,
时, ,不合题意;
,不合题意;
综上,实数 的取值范围是
的取值范围是

练习册系列答案
相关题目
 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 的值域是
的值域是 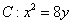 与直线
与直线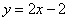 相交于
相交于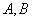 两点,点
两点,点 是抛物线
是抛物线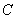 上不同
上不同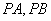 分别与直线
分别与直线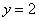 相交于点
相交于点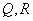 ,
,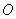 为坐标原点,则
为坐标原点,则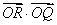 的值是
的值是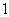 的等比数列
的等比数列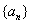 的首项
的首项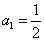 ,前
,前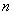 项和为
项和为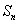 ,且
,且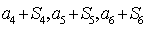 成等差数列.
成等差数列.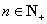 ,在
,在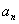 与
与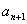 之间插入
之间插入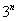 个数,使这
个数,使这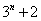 个数成等差数列,记插入的这
个数成等差数列,记插入的这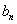 ,求数列
,求数列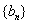 的前
的前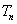 .
. ,则
,则 是
是 的( ).
的( ). 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足 ,且
,且 ,(其中
,(其中 为
为 项和),则
项和),则 ( ).
( ). B.
B. C.
C. D.
D.
 cm3 B.
cm3 B. cm3 C.
cm3 C. cm3 D.
cm3 D. cm3
cm3