题目内容

设P是△ABC所在平面上一点，且满足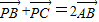，若△ABC的面积为1，则△PAB的面积为（ ）
A．
B．
C．1
D．2
【答案】分析：取BC的中点D，则，由条件可得四边形ABDP是平行四边形，根据BC的中点D，可得P到AB的距离为C到AB距离的一半．由此可得结论．
解答：解：取BC的中点D，则

∵
∴
∴四边形ABDP是平行四边形
∵BC的中点D，∴P到AB的距离为C到AB距离的一半
∵△ABC的面积为1，∴△PAB的面积为
故选B．
点评：本题考查向量的运算，考查三角形面积的计算，确定P到AB的距离为C到AB距离的一半是关键．
练习册系列答案
相关题目
设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则（　　）
A、
PA
+
PB
=
0
B、
PC
+
PA
=
0
C、
PB
+
PC
=
0
D、
PA
+
PB
+
PC
=
0
24、设P是△ABC所在平面外一点，P和A、B、C的距离相等，∠BAC为直角．
求证：平面PCB⊥平面ABC．
设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则（　　）
设P是△ABC所在平面上的一点，
AP
=
1
3
AB
+t
AC
，(t∈R)，使P落在△ABC内部（不含边界）的t的取值范围是
(0，
2
3
)
(0，
2
3
)
．
设P是△ABC所在平面α外一点，H是P在α内的射影，且PA，PB，PC与α所成的角相等，则H是△ABC的（　　）
A、内心B、外心C、垂心D、重心

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网