题目内容
[2014·宁波质检]化简Sn=n+(n-1)×2+(n-2)×22+…+2×2n-2+2n-1的结果是( )
| A.2n+1-n | B.2n+1-n+2 |
| C.2n-n-2 | D.2n+1-n-2 |
D
解析

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
数列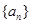 的通项公式
的通项公式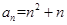 ,则数列
,则数列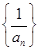 的前10项和为( )
的前10项和为( )
A.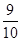 | B.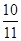 | C.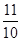 | D.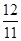 |
设等差数列 的前n项和为
的前n项和为 ,若
,若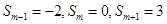 ,则
,则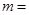 ( )
( )
| A.3 | B.4 | C.5 | D.6 |
数列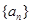 的通项公式为
的通项公式为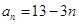 ,
,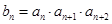 ,
,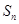 是数列
是数列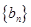 的前
的前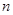 项和,则
项和,则 的最大值为( )
的最大值为( )
| A.280 | B.300 | C.310 | D.320 |
在数列{an}中,已知a1 = 2,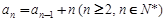 ,则a4等于( )
,则a4等于( )
| A.4 | B.11 | C.10 | D.8 |
已知函数f(n)= ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
| A.-2013 | B.-2014 | C.2013 | D.2014 |
已知函数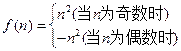 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
| A.0 |
| B.100 |
| C.-100 |
| D.10200 |
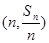 在直线
在直线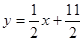 上.数列{bn}满足
上.数列{bn}满足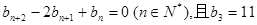 ,前9项和为153.
,前9项和为153.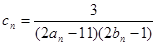 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式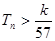 对一切
对一切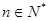 都成立的最大正整数k的值.
都成立的最大正整数k的值. 和
和 满足:
满足: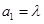 ,
,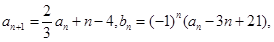 其中
其中 为实数,
为实数,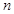 为正整数.
为正整数. ;
;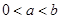 ,是否存在实数
,是否存在实数 成立? 若存在,求
成立? 若存在,求