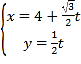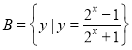题目内容
【题目】定义:如果存在实常数a和b,使得函数![]() 总满足
总满足![]() ,我们称这样的函数
,我们称这样的函数![]() 是“
是“![]() 型函数”.请解答以下问题:
型函数”.请解答以下问题:
(1)已知函数![]() 是“
是“![]() 型函数”,求p和b的值;
型函数”,求p和b的值;
(2)已知函数![]() 是“
是“![]() 型函数”,求一组满足条件的k、m和a的值,并说明理由.
型函数”,求一组满足条件的k、m和a的值,并说明理由.
(3)已知函数![]() 是一个“
是一个“![]() 型函数”,且
型函数”,且![]() ,
,![]() 是增函数,若
是增函数,若![]() 是
是![]() 在区间
在区间![]() 上的图像上的点,求点M随着
上的图像上的点,求点M随着![]() 变化可能到达的区域的面积的大小,并证明你的结论.
变化可能到达的区域的面积的大小,并证明你的结论.
【答案】(1)![]() (2)
(2)![]() ,
,![]() ,
,![]() ,理由见解析 (3)M点在不等式
,理由见解析 (3)M点在不等式![]() (
(![]() 时等号不成立)所表示的区域内,面积为4,证明见解析
时等号不成立)所表示的区域内,面积为4,证明见解析
【解析】
(1)由函数![]() 是“
是“![]() 型函数”,则有
型函数”,则有![]() ,将函数表达式代入可求出
,将函数表达式代入可求出![]() 的值.
的值.
(2)先证明![]() 的图像是关于
的图像是关于![]() 对称的,然后根据
对称的,然后根据![]() 是“
是“![]() 型函数”求出一组满足条件的k、m和a的值即可.
型函数”求出一组满足条件的k、m和a的值即可.
(3)由函数![]() 是一个“
是一个“![]() 型函数”,且
型函数”,且![]() ,
,![]() 是增函数,可得M点在不等式
是增函数,可得M点在不等式![]() (
(![]() 时等号不成立)所表示的区域内,在证明其充要性.
时等号不成立)所表示的区域内,在证明其充要性.
(1)解:![]() ,
,
所以![]() ,即
,即![]()
(2)解:设![]()
注意到![]() 的图像是轴对称图形,
的图像是轴对称图形,![]() 的对称轴是
的对称轴是![]() ,证明如下,
,证明如下,
因为![]()
![]() ,
,
即![]() ;
;
![]()
![]() ,
,
于是![]() ,
,![]() ,此时
,此时![]() .
.
(3)解:M点在不等式![]() (
(![]() 时等号不成立)所表示的区域内;
时等号不成立)所表示的区域内;
所以在![]() 的面积为
的面积为![]()
下面证明:
![]() M点在不等式
M点在不等式![]() (
(![]() 时等号不成立)所表示的区域内;
时等号不成立)所表示的区域内;
![]() ,
,![]() ,
,![]() 时,
时,![]() ,满足
,满足![]()
由![]() 单调递增,得到
单调递增,得到![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
此时![]() ,
,![]() ,所以满足
,所以满足![]()
当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]()
此时![]() ,
,![]() ,所以满足
,所以满足![]()
即M点在不等式![]() (
(![]() 时等号不成立)所表示的区域内
时等号不成立)所表示的区域内
(B)证明:M点可为![]() (
(![]() 时等号不成立)所表示的区域内任意点.
时等号不成立)所表示的区域内任意点.
存在函数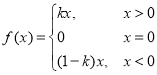 ,此时
,此时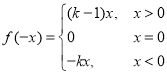 ,
,
其中![]() ,此时
,此时![]() 是增函数,并满足
是增函数,并满足![]() .
.
让k在区间![]() 变化,
变化,![]() 图像充满
图像充满![]() (
(![]() 时等号不成立)所在区域
时等号不成立)所在区域
由A、B得:M运动区域是![]() (
(![]() 时等号不成立)所在区域.
时等号不成立)所在区域.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目