Question

已知sin(α+β)=,sin(α-β)=,求的值.

Answer 1

思路分析：两角和与差的正弦公式很相似，只差一个符号，若将sin(α+β)=和sin(α-β)=展开，联立成方程就可以求出sinαcosβ和cosαsinβ，那么这两者之比就是所要求的结果.

解：∵sin(α+β)=,∴sinαcosβ+cosαsinβ=.                     ①

又∵sin(α-β)=,∴sinαcosβ-cosαsinβ=.                          ②

①+②得sinαcosβ=.

①-②得cosαsinβ=.

∴.

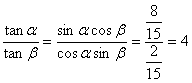方法归纳 在应用两角和与差的正弦公式解题时，一定要注意已知条件和所要求的结论之间的内在联系，以及在解题时选择适当的公式和解题方法.