题目内容
在△ABC中,已知
=
,则cosA=
.
| tanA |
| tanB |
| ||
| b |
| ||
| 2 |
| ||
| 2 |
分析:已知等式左边利用同角三角函数间的基本关系化简,再利用正弦定理变形,整理后根据图形得到acosB+bcosA=c,变形即可求出cosA的值.
解答: 解:根据正弦定理化简已知等式得:
解:根据正弦定理化简已知等式得:
=
=
•
=
,即(
c-b)cosA=acosB,
整理得:
c•cosA=acosB+bcosA=c,
则cosA=
.
故答案为:
 解:根据正弦定理化简已知等式得:
解:根据正弦定理化简已知等式得:| tanA |
| tanB |
| ||
|
| a |
| b |
| cosB |
| cosA |
| ||
| b |
| 2 |
整理得:
| 2 |
则cosA=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题考查了正弦定理,以及同角三角函数间的基本关系,画出相应的图形是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.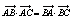 .
. |=|
|=| |;
|; ,求|
,求| -t
-t