题目内容
已知O为正方形ABCD的中心，点P为正方形ABCD所在平面外一点，若
+
+
+
=λ
，则λ=（ ）
| PA |
| PB |
| PC |
| PD |
| PO |
分析：根据向量的三角形法则，将
，
，
，
均转化成
表示，再利用O为正方形ABCD的中心，则
+
=
，
+
=
，从而得到
+
+
+
=4
，即可得到λ的值．
| PA |
| PB |
| PC |
| PD |
| PO |
| OA |
| OC |
| 0 |
| OB |
| OD |
| 0 |
| PA |
| PB |
| PC |
| PD |
| PO |
解答：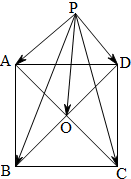
解：∵O为正方形ABCD的中心，
∴
+
=
，
而
=
+
，
=
+
，
∴
+
=2
+
+
=2
，
同理：
+
=2
，
∴
+
+
+
=4
，
即λ=4．
故选D．
解：∵O为正方形ABCD的中心，∴
| OA |
| OC |
| 0 |
而
| PA |
| PO |
| OA |
| PC |
| PO |
| OC |
∴
| PA |
| PC |
| PO |
| OA |
| OC |
| PO |
同理：
| PB |
| PD |
| PO |
∴
| PA |
| PB |
| PC |
| PD |
| PO |
即λ=4．
故选D．
点评：本题主要考查了向量在几何中的应用，解题的关键是运用向量加法和减法的三角形法则，将向量进行合理的转化，转化的关键是该往哪些向量转化，一般是向已知的向量进行转化，向需要的向量进行转化．属于中档题．
练习册系列答案
相关题目
已知正方形ABCD的边长为2
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
已知边长为2的正方形ABCD，E，F分别是AB，CD的中点，将△ADE沿DE折起，点A在平面BCDE的投影点O恰好落在直线EF上．
