题目内容
已知函数 ,
, .
.
(Ⅰ)若 与
与 在
在 处相切,试求
处相切,试求 的表达式;
的表达式;
(Ⅱ)若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅲ)证明不等式:

 .
.
(Ⅰ)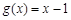 ;(Ⅱ)
;(Ⅱ) .(Ⅲ)见解析
.(Ⅲ)见解析
解析试题分析:(Ⅰ)求导数,利用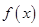 与
与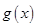 在
在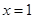 处相切,可求
处相切,可求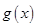 的表达式;(Ⅱ)
的表达式;(Ⅱ)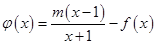 在
在 上是减函数,可得导函数小于等于
上是减函数,可得导函数小于等于 在
在 上恒成立,分离参数,利用基本不等式,可求实数
上恒成立,分离参数,利用基本不等式,可求实数 的取值范围;(Ⅲ)当x≥2时,证明
的取值范围;(Ⅲ)当x≥2时,证明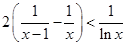 ,当x>1时,证明
,当x>1时,证明 ,利用叠加法,即可得到结论.
,利用叠加法,即可得到结论.
试题解析:解:(Ⅰ)由已知 且
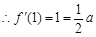 得:
得: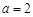 2分
2分
又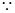




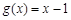 3分
3分
(Ⅱ)

 在
在 上是减函数,
上是减函数,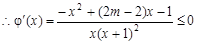 在
在 上恒成立. 5分
上恒成立. 5分
即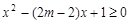 在
在 上恒成立,由
上恒成立,由 ,
,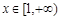

 得
得 6分
6分
(Ⅲ)由(Ⅰ)可得:当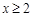 时:
时:
 得:
得: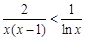
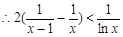 8分
8分
当 时:
时: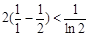 当
当 时:
时: 当
当 时:
时:
当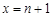 时:
时: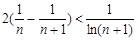 ,
,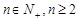
上述不等式相加得:
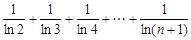
即:
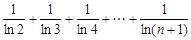 ① 9分
① 9分
由(Ⅱ)可得:当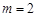 时:
时:

 在
在 上是减函数
上是减函数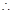 当
当 时:
时: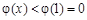 即
即
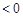
所以 从而得到:
从而得到:
练习册系列答案
相关题目
 .若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格). ,函数
,函数 .
. 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围. ,其中
,其中
 是自然对数的底数.
是自然对数的底数.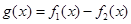 的零点;
的零点;
 均有两个极值点,一个在区间
均有两个极值点,一个在区间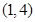 内,另一个在区间
内,另一个在区间 外,
外, 的取值范围;
的取值范围; 且函数
且函数 在
在 上是单调函数,探究函数
上是单调函数,探究函数 的单调性.
的单调性.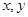 )为函数
)为函数 图像上一点,O为坐标原点,记直线OP的斜率
图像上一点,O为坐标原点,记直线OP的斜率 。
。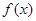 的单调区间;
的单调区间; ,求函数
,求函数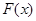 的最小值。
的最小值。 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。 为实常数,函数
为实常数,函数 .
. 的单调性;
的单调性; ;
; 且
且 .(注:
.(注: 为自然对数的底数)
为自然对数的底数) ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于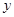 轴.
轴. 的值;
的值; 的极值.
的极值.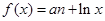 ,其中实数a为常数.
,其中实数a为常数. 的单调区间:
的单调区间: (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值; .
.