题目内容
设点F1,F2分别为椭圆 的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是________.
的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是________.

分析:欲求椭圆离心率e的取值范围,关键是建立a,c之间的不等关系,设M(x,y)利用MF₁,MF₂,d成等比数列,得出
 =
= ,由于M在椭圆上,故-a≤x≤a,即有-1≤x/a≤1,从而得到不等关系-1≤
,由于M在椭圆上,故-a≤x≤a,即有-1≤x/a≤1,从而得到不等关系-1≤ ≤1;解之即可得到e的取值范围.
≤1;解之即可得到e的取值范围.解答:设M(x,y);l为右准线;
故MF₂=r₂=a-ex; MF₁=r₁=2a-r₂=2a-(a-ex)=a+ex;
MF₁,MF₂,d成等比数列,故有:r2₂=dr₁,
即有(a-ex)2=(a+ex)(a-ex)/e,
化简得e(a-ex)=a+ex,故
 =
= ,
,由于M在椭圆上,故-a≤x≤a,即有-1≤x/a≤1,
∴-1≤
 ≤1;由于e-1<0,
≤1;由于e-1<0,故只需考虑不等式的左边,即考虑-1≤
 ,-e(e+1)≤e-1,
,-e(e+1)≤e-1,∴e2+2e-1≧0,故得e≥
 ,
,即e的取值范围为
 .
.故答案为:
 .
.点评:本小题主要考查椭圆的简单性质、等比数列的性质、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
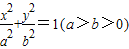 的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是 .
的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是 .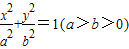 的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是 .
的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是 .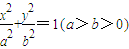 的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是 .
的左,右两焦点,直线l为右准线.若在椭圆上存在点M,使MF1,MF2,点M到直线l的距离d成等比数列,则此椭圆离心率e的取值范围是 .