题目内容
设点F1，F2分别为椭圆C：
+
=1的左、右焦点，点P为椭圆C上任意一点，则使得
•
=2成立的点P的个数为（ ）
| x2 |
| 9 |
| y2 |
| 5 |
| PF1 |
| PF2 |
分析：设P（x0，y0），由
•
=2，得x02+y02=6①，由点P在椭圆上，得
+
=1②，联立①②可解方程组．
| PF1 |
| PF2 |
| x02 |
| 9 |
| y02 |
| 5 |
解答：解：设P（x0，y0），则
=（-2-x0，-y0），
=（2-x0，-y0），
由
•
=2，得（-2-x0，-y0）•（2-x0，-y0）=2，即x02+y02=6①，
又点P在椭圆上，所以
+
=1②，
联立①②解得
或
或
或
，
故满足题意的点P有4个，
故选D．
| PF1 |
| PF2 |
由
| PF1 |
| PF2 |
又点P在椭圆上，所以
| x02 |
| 9 |
| y02 |
| 5 |
联立①②解得
|
|
|
|
故满足题意的点P有4个，
故选D．
点评：本题考查平面向量数量积的运算、椭圆的简单性质，考查方程思想，属中档题．
练习册系列答案
相关题目
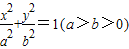的左，右两焦点，直线l为右准线．若在椭圆上存在点M，使MF1，MF2，点M到直线l的距离d成等比数列，则此椭圆离心率e的取值范围是 ．
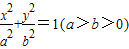的左，右两焦点，直线l为右准线．若在椭圆上存在点M，使MF1，MF2，点M到直线l的距离d成等比数列，则此椭圆离心率e的取值范围是 ．
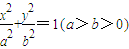的左，右两焦点，直线l为右准线．若在椭圆上存在点M，使MF1，MF2，点M到直线l的距离d成等比数列，则此椭圆离心率e的取值范围是 ．