题目内容
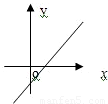
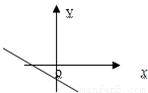
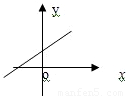
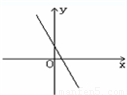
若函数f(x)=x2+bx+c的图象的顶点在第四象限,则函数f′(x)的图象是( )A.
B.
C.
D.
【答案】分析:先判断函数f(x)的单调性,根据当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减得到答案.
解答:解:函数f(x)=x2+bx+c是开口向上的二次函数,顶点在第四象限说明对称轴大于0
根据函数f(x)在对称轴左侧单调递减,导函数小于0;在对称轴右侧单调递增,导函数大于0知,A满足条件
故选A.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.
解答:解:函数f(x)=x2+bx+c是开口向上的二次函数,顶点在第四象限说明对称轴大于0
根据函数f(x)在对称轴左侧单调递减,导函数小于0;在对称轴右侧单调递增,导函数大于0知,A满足条件
故选A.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目