题目内容
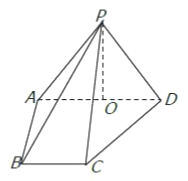
【题目】已知四棱锥P-ABCD的体积为![]() ,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.
,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.

(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据四棱锥的体积得PA=![]() ,进而得正视图的面积;
,进而得正视图的面积;
(2)过A作AE∥CD交BC于E,连接PE,确定四个侧面积面积S△PAB,S△PAD, S△PCD, S△PBC求和即可.
试题解析:
(1) 如图所示四棱锥P-ABCD的高为PA,底面积为S=![]() ·CD=
·CD=![]() ×1=
×1=![]()
∴四棱锥P-ABCD的体积V四棱锥P-ABCD=![]() S·PA=
S·PA=![]() ×
×![]() ·PA=
·PA=![]() ,∴PA=
,∴PA=![]()
∴正视图的面积为S=![]() ×2×
×2×![]() =
=![]() .
.
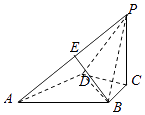
(2)如图所示,过A作AE∥CD交BC于E,连接PE.根据三视图可知,E是BC的中点,
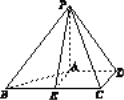
且BE=CE=1,AE=CD=1,且BC⊥AE,AB=![]()
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD=![]() ,∴BC⊥面PAE,∴BC⊥PE,
,∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE=![]() .
.
∴四棱锥P-ABCD的侧面积为
S=S△PAB+ S△PAD+ S△PCD+ S△PBC=![]() ·
·![]() ·
·![]() +
+![]() ·
·![]() ·1+
·1+![]() ·1·
·1·![]() +
+![]() ·2·
·2·![]() =
=![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目