题目内容
已知函数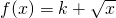 ,存在区间[a,b]⊆[0,+∞),使f(x)在[a,b]上的值域仍是[a,b],求实数k的取值范围.
,存在区间[a,b]⊆[0,+∞),使f(x)在[a,b]上的值域仍是[a,b],求实数k的取值范围.
解:函数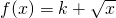 在[0,+∞)上为增函数
在[0,+∞)上为增函数
f(x)在[a,b](⊆[0,+∞))上的值域为[a,b],其充要条件是
? ?b>a≥0,
?b>a≥0,
 、
、 是方程t2-t-k=0的两个不相等的非负实根.
是方程t2-t-k=0的两个不相等的非负实根.
故存在[a,b](⊆[0,+∞)),使f(x)在[a,b]上的值域为[a,b]的充要条件
是 ?
?
分析:根据函数的单调性以及f(x)在[a,b]上的值域仍是[a,b]建立等式关系,从而可知 、
、 是方程t2-t-k=0的两个不相等的非负实根,然后建立关系式即可.
是方程t2-t-k=0的两个不相等的非负实根,然后建立关系式即可.
点评:本题主要考查了函数的值域,以及函数的单调性和充要条件的理解,属于中档题.
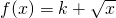 在[0,+∞)上为增函数
在[0,+∞)上为增函数f(x)在[a,b](⊆[0,+∞))上的值域为[a,b],其充要条件是

?
 ?b>a≥0,
?b>a≥0, 、
、 是方程t2-t-k=0的两个不相等的非负实根.
是方程t2-t-k=0的两个不相等的非负实根.故存在[a,b](⊆[0,+∞)),使f(x)在[a,b]上的值域为[a,b]的充要条件
是
 ?
?
分析:根据函数的单调性以及f(x)在[a,b]上的值域仍是[a,b]建立等式关系,从而可知
 、
、 是方程t2-t-k=0的两个不相等的非负实根,然后建立关系式即可.
是方程t2-t-k=0的两个不相等的非负实根,然后建立关系式即可.点评:本题主要考查了函数的值域,以及函数的单调性和充要条件的理解,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 定义在区间
定义在区间 ,对任意
,对任意 ,恒有
,恒有 成立,又数列
成立,又数列 满足
满足 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得 (II)求证:数列
(II)求证:数列 是等比数列,并求
是等比数列,并求 的表达式;(III)设
的表达式;(III)设 ,是否存在
,是否存在 ,使得对任意
,使得对任意 ,
, 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。 的减区间是
的减区间是 .
. 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;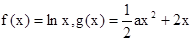 ,若
,若 存在单调减区间,则实数
存在单调减区间,则实数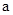 的取值范围是( )
的取值范围是( ) B.(0,1) C.(-1,0) D.
B.(0,1) C.(-1,0) D.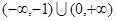
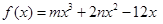 的减区间是
的减区间是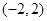 .
.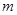 、
、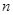 的值;
的值;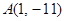 且与曲线
且与曲线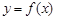 相切的切线方程;
相切的切线方程; 是否存在与曲线
是否存在与曲线