题目内容
已知函数f（x）=x+
．
（1）判断函数的奇偶性，并加以证明；
（2）用定义证明f（x）在（0，1）上是减函数；
（3）写出函数f（x）在整个定义域上的单调区间．（直接写出答案，不要求写证明过程）．
解：（1）函数为奇函数，
证明：因为f（x）的定义域为{x|x≠0}，
且f（-x）=-x-=-（x+）=-f（x），
所以f（x）为奇函数；
（2）设x1，x2∈（0，1）且设x1＜x2，
则f（x1）-f（x2）=（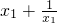
）-（x2+
）=
，
∵0＜x1＜x2＜1，∴0＜x1x2＜1，x1x2-1＜0，x1-x2＜0，
∴f（x1）-f（x2）＞0，即f（x1）＞f（x2）．
所以函数f（x）在（0，1）上是减函数．
（3）函数f（x）在（-∞，-1）上是增函数，在（-1，0）上是减函数，
在（0，1）上是减函数，在（1，+∞）上是增函数．
分析：（1）根据函数奇偶性的定义即可判断、证明；
（2）设x1，x2∈（0，1）且设x1＜x2，根据减函数的定义利用作差证明f（x1）＞f（x2）即可；
（3）可以根据函数图象直接写出；
点评：本题考查函数的奇偶性、单调性的判断证明，属基础题，定义是解决该类问题的基本方法．
证明：因为f（x）的定义域为{x|x≠0}，
且f（-x）=-x-
=-（x+）=-f（x），所以f（x）为奇函数；
（2）设x1，x2∈（0，1）且设x1＜x2，
则f（x1）-f（x2）=（
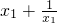）-（x2+）=，∵0＜x1＜x2＜1，∴0＜x1x2＜1，x1x2-1＜0，x1-x2＜0，
∴f（x1）-f（x2）＞0，即f（x1）＞f（x2）．
所以函数f（x）在（0，1）上是减函数．
（3）函数f（x）在（-∞，-1）上是增函数，在（-1，0）上是减函数，
在（0，1）上是减函数，在（1，+∞）上是增函数．
分析：（1）根据函数奇偶性的定义即可判断、证明；
（2）设x1，x2∈（0，1）且设x1＜x2，根据减函数的定义利用作差证明f（x1）＞f（x2）即可；
（3）可以根据函数图象直接写出；
点评：本题考查函数的奇偶性、单调性的判断证明，属基础题，定义是解决该类问题的基本方法．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|