题目内容
已知函数f（x）=x2-4|x|+3+m有两个零点，则m的取值范围为（ ）A．
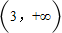
B．
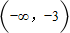
C．
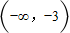∪{1}D．
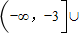{1}
【答案】分析：分类讨论，去掉绝对值，化简函数的解析式，根据函数的图象利用数形结合的方法进行求解；
解答：解：∵函数f（x）=x2-4|x|+3+m，
∴f（x）=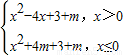
，
∵函数f（x）=x2-4|x|+3+m有两个零点，两个方程判别式值一样，
①在（0，+∞）和（-∞，0）上各有一个根，
∴△=16-4（3+m）=0，解得m=1；
②第二种情况：如下图：画出函数f（x）=|x|2-4|x|+3+m的图象，
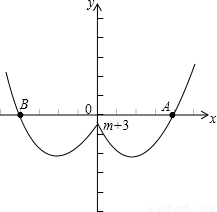
f（x）是偶函数，此时只要与y轴的交点小于0，即可，
∴
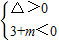解得m＜-3，
综上：m的范围为：（-∞，-3）∪{1}
故选C；
点评：本题考查函数零点的求法，以及函数零点存在的条件，体现了分类讨论的数学思想，属于基础题．
解答：解：∵函数f（x）=x2-4|x|+3+m，
∴f（x）=
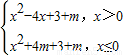，∵函数f（x）=x2-4|x|+3+m有两个零点，两个方程判别式值一样，
①在（0，+∞）和（-∞，0）上各有一个根，
∴△=16-4（3+m）=0，解得m=1；
②第二种情况：如下图：画出函数f（x）=|x|2-4|x|+3+m的图象，
f（x）是偶函数，此时只要与y轴的交点小于0，即可，
∴
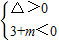解得m＜-3，综上：m的范围为：（-∞，-3）∪{1}
故选C；
点评：本题考查函数零点的求法，以及函数零点存在的条件，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|