题目内容
已知抛物线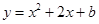
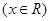 与坐标轴有三个交点,经过这三点的圆记为
与坐标轴有三个交点,经过这三点的圆记为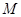 .
.
(1)求实数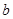 的取值范围;
的取值范围;
 (2)设抛物线与x轴的交点从左到右分别为A、B,与y轴的交点为C,求A、B、C三点的坐标;
(2)设抛物线与x轴的交点从左到右分别为A、B,与y轴的交点为C,求A、B、C三点的坐标;
(3)设直线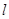 是抛物线在点A处的切线,试判断直线
是抛物线在点A处的切线,试判断直线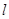 是否也是圆
是否也是圆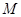 的切线?并说明理由.
的切线?并说明理由.
直线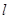 不可能是圆
不可能是圆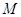 的切线.
的切线.
【解析】解:(1)∵抛物线与坐标轴有三个交点∴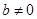 ,否则抛物线与坐标轴只有两个交点,与题设不符,由
,否则抛物线与坐标轴只有两个交点,与题设不符,由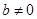 知,抛物线与y轴有一个非原点的交点
知,抛物线与y轴有一个非原点的交点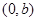 ,故抛物线与x轴有两个不同的交点,即方程
,故抛物线与x轴有两个不同的交点,即方程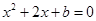 有两个不同的实根
有两个不同的实根
∴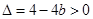 即
即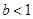
∴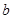 的取值范围是
的取值范围是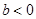 或
或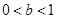 -----------------------------------3分
-----------------------------------3分
(2)令x=0得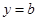 ,∴
,∴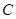
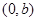 ---------------------------------4分
---------------------------------4分
令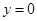 得
得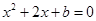 解得
解得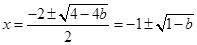
∴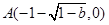 ,
,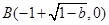 ------------------------------6分
------------------------------6分
(3)解法1:∵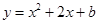 ∴
∴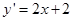
∴直线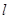 的斜率
的斜率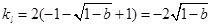 -----------------------7分
-----------------------7分
∵圆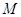 过A、B、C三点,∴圆心M为线段AB与AC的垂直平分线的交点
过A、B、C三点,∴圆心M为线段AB与AC的垂直平分线的交点
∵AB的垂直平分线即抛物线的对称轴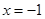
∵线段AC的中点为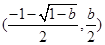 直线AC的斜率
直线AC的斜率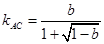
∴线段AC的垂直平分线方程为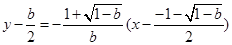 ---(
---( )----10分
)----10分
将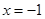 代入(
代入(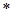 )式解得
)式解得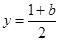 ,即
,即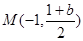 ------------------------11分
------------------------11分
∴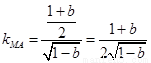 ,若直线
,若直线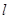 也是圆
也是圆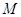 的切线,则
的切线,则
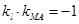 即
即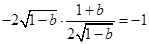
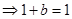 解得
解得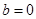
这与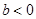 或
或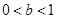 矛盾 ----------------------------------------13分
矛盾 ----------------------------------------13分
∴直线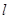 不可能是圆
不可能是圆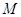 的切线. -----------------------------------14分
的切线. -----------------------------------14分
解法2:∵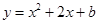 ∴
∴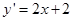
∴直线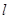 的斜率
的斜率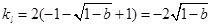 ---------------------------7分
---------------------------7分
设圆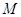 的方程为
的方程为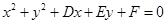
∵圆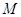 过
过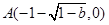 ,
,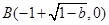 ,
,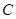
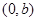
∴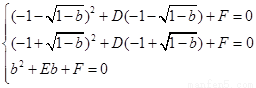 解得
解得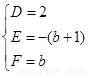 ------------10分
------------10分
∴圆心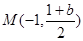 -------------------------------------------------11分
-------------------------------------------------11分
∴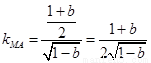 ,若直线
,若直线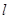 也是圆
也是圆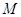 的切线,则
的切线,则
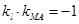 即
即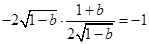
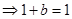 解得
解得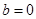
这与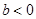 或
或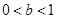 矛盾----------------------------------------13分
矛盾----------------------------------------13分
∴直线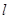 不可能是圆
不可能是圆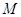 的切线.-----------------------------------14分
的切线.-----------------------------------14分

 全优点练单元计划系列答案
全优点练单元计划系列答案