题目内容
已知圆O的半径为
,圆周上两点A、B与原点O恰构成正三角形,则向量
与
的数量积是( )
| 3 |
| OA |
| OB |
分析:利用数量积的定义先确定向量量
与
的夹角,然后利用公式进行求解即可.
| OA |
| OB |
解答:解:∵圆周上两点A、B与原点O恰构成正三角形,
∴向量
与
的夹角为
,且|
|=|
|=
,
∴向量
与
的数量积
•
=|
|•|
|cos
=
•
•
=
.
故选C.
∴向量
| OA |
| OB |
| π |
| 3 |
| OA |
| OB |
| 3 |
∴向量
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| π |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
故选C.
点评:本题主要考查平面向量数量积的定义及计算,利用正三角形确定向量夹角是解决本题的关键.

练习册系列答案
相关题目
 已知圆O的半径为3,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为2
已知圆O的半径为3,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为2 (几何证明选讲选做题)如图,PC切圆O于点C,割线PAB经过圆O,弦CD⊥AB于点E,已知圆O的半径为3,PA=2,则PC=
(几何证明选讲选做题)如图,PC切圆O于点C,割线PAB经过圆O,弦CD⊥AB于点E,已知圆O的半径为3,PA=2,则PC=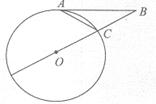
 ,AB=3,则切线AD的长为___ _____.
,AB=3,则切线AD的长为___ _____.