题目内容
 已知圆O的半径为3,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为2
已知圆O的半径为3,从圆O外一点A引切线AD和割线ABC,圆心O到AC的距离为2| 2 |
分析:由已知中圆O的半径为3,圆心O到AC的距离为2
,由半径长、弦心距、半弦长构成直角三角形,满足勾股定理,我们易求出BC的长,进而求出AC长,由切割线定理,得到切线AD的长.
| 2 |
解答:解:∵圆O的半径为3,
圆心O到AC的距离为2
∴BC=2
=2
又∵AB=3,∴AC=5
又∵AD为圆O的切线
ABC为圆O的割线
由切割线定理得:
AD2=AB•AC=3×5=15
∴AD=
圆心O到AC的距离为2
| 2 |
∴BC=2
32-(2
|
又∵AB=3,∴AC=5
又∵AD为圆O的切线
ABC为圆O的割线
由切割线定理得:
AD2=AB•AC=3×5=15
∴AD=
| 15 |
点评:本题考查的知识点是弦长公式,切割线定理,其中根据半径长、弦心距、半弦长构成直角三角形,满足勾股定理,求出BC的长,是解答本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (几何证明选讲选做题)如图,PC切圆O于点C,割线PAB经过圆O,弦CD⊥AB于点E,已知圆O的半径为3,PA=2,则PC=
(几何证明选讲选做题)如图,PC切圆O于点C,割线PAB经过圆O,弦CD⊥AB于点E,已知圆O的半径为3,PA=2,则PC=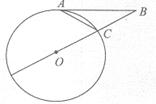
 ,AB=3,则切线AD的长为___ _____.
,AB=3,则切线AD的长为___ _____.