题目内容
(1)已知圆C:x2+y2+Dx+Ey+3=0,圆C关于直线x+y﹣1=0对称,圆心在第二象限,半径为![]() .求圆C的方程;
.求圆C的方程;
(2)已知圆C:x2+y2=4.直线l过点P(1,2),且与圆C交于A、B两点,若![]() ,求直线l的方程.
,求直线l的方程.
考点:
直线与圆相交的性质;直线和圆的方程的应用.
专题:
综合题;直线与圆.
分析:
(1)确定圆心坐标与半径,利用圆C关于直线x+y﹣1=0对称,圆心在第二象限,半径为![]() ,求出D,E,即可求圆C的方程;
,求出D,E,即可求圆C的方程;
(2)分类讨论,利用圆的弦长公式,即可求得直线l的方程.
解答:
解:(1)由题意圆心坐标为(﹣![]() ,﹣
,﹣![]() ),半径为
),半径为![]()
∵圆C关于直线x+y﹣1=0对称,半径为![]()
∴![]() ,
,![]()
∴D=2,E=﹣4或D=﹣4,E=2
∵圆心在第二象限,
∴圆心坐标为(﹣1,2)
∴圆C的方程为x2+y2+2x﹣4y+3=0;
(2)当直线的斜率不存在时,方程为x=1,A(1,![]() ),B(1,﹣
),B(1,﹣![]() ),
),![]() ,满足题意;
,满足题意;
当直线的斜率存在时,设方程为y﹣2=k(x﹣1),即kx﹣y﹣k+2=0
圆心到直线的距离为d=![]()
∵![]() ,∴
,∴![]()
∴k=![]()
∴![]() ,即3x﹣4y+5=0.
,即3x﹣4y+5=0.
点评:
本题考查圆的方程,考查待定系数法,考查圆中弦长的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
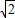 .求圆C的方程;
.求圆C的方程; ,求直线l的方程.
,求直线l的方程.