题目内容
设满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”:
阶“期待数列”:
①![]() ,②
,②![]() .
.
(Ⅰ)若等比数列![]() 为
为![]() 阶“期待数列”,求公比
阶“期待数列”,求公比![]() ;
;
(Ⅱ)若一个等差数列![]() 既是
既是![]() 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(Ⅲ)记![]() 阶“期待数列”
阶“期待数列”![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求证: ![]() ;
;
(2)若存在![]() ,使
,使![]() ,试问数列
,试问数列![]() 能否为
能否为![]() 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
解: (Ⅰ) 若![]() ,则 由①
,则 由①![]() 得
得![]() ,
,
由②得![]() 或
或![]() . 若
. 若![]() ,由①得,
,由①得, ![]() ,得
,得![]() ,不可能.
,不可能.
综上所述![]() .
.
(Ⅱ)设等差数列![]() 的公差为
的公差为![]() .
.
因为![]() ,所以
,所以![]() .所以
.所以![]() .
.
因为![]() ,所以由
,所以由![]() 得
得![]() .
.
由题中的①、②得
![]() ,
, ![]() ,
,
两式相减得![]() , 即
, 即![]() . 又
. 又![]() ,得
,得![]() .
.
所以![]() .
.
(Ⅲ) 记![]() 中非负项和为
中非负项和为![]() ,负项和为
,负项和为![]() .
.
则![]() , 得
, 得![]() .
.
(1) 因为![]() ,
,
所以![]() .
.
(2) 若存在![]() ,使
,使![]() ,由前面的证明过程知:
,由前面的证明过程知:
![]() ,
,
且![]() .
.
记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
则由(1)知, ![]() .
.
所以![]()
因为![]() ,
,
所以![]() .
.
所以![]() ,
,![]() .
.
又![]() ,
,
则![]() .
.
所以![]() .
.
所以![]() 与
与![]() 不能同时成立.
不能同时成立.
所以对于有穷数列![]()
![]() ,
,
若存在![]() ,使
,使![]() ,
,
则数列![]() 不能为
不能为![]() 阶“期待数列”.
阶“期待数列”.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目

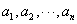 为
为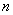
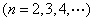 阶“期待数列”:
阶“期待数列”: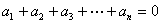 ;②
;②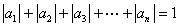 .
.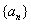 为
为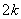 (
(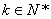 )阶“期待数列”,求公比
)阶“期待数列”,求公比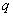 ;
;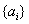 的前
的前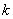 项和为
项和为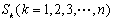 :
: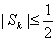 ;
;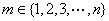 使
使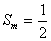 ,试问数列
,试问数列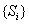 能否为
能否为