题目内容
1.若“x2>1”是“x<a”的必要不充分条件,则a的取值范围是(-∞,-1].分析 由x2>1得x<-1或x>1,又“x2>1”是“x<a”的必要不充分条件,知“x<a”可以推出“x2>1”,反之不成立.由此可求出a的范围.
解答 解:由x2>1得x<-1或x>1,又“x2>1”是“x<a”的必要不充分条件,
知“x<a”可以推出“x2>1”,
反之不成立.
则a的最大值为-1.
∴a≤-1
故答案为:(-∞,-1].
点评 本题考查必要条件、充分条件、充要条件的判断,解题时要认真审题,仔细解答.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
11.直线$\sqrt{3}$x-y-3=0的倾斜角是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
12.若a,b∈R,则a(a-b)>0是$\frac{b}{a}<1$成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.复数$\frac{5}{1-2i}$(i为虚数单位)的虚部是( )
| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
16.已知sin($\frac{π}{4}$-x)=$\frac{4}{5}$,则sin2x=( )
| A. | $\frac{18}{25}$ | B. | $\frac{7}{25}$ | C. | -$\frac{7}{25}$ | D. | -$\frac{16}{25}$ |
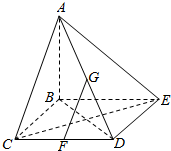 在四棱锥A-BCDE中,AB⊥平面BCDE,底面BCDE是正方形且AB=CD,点G,F分别是AD和CD的中点.求:
在四棱锥A-BCDE中,AB⊥平面BCDE,底面BCDE是正方形且AB=CD,点G,F分别是AD和CD的中点.求: