Question

经过随机抽样，得到1000名高三学生体重的基本情况，如下表：

	偏瘦	正常	偏胖
女生（人）	100	173	b
男生（人）	150	177	c

（1）根据研究需要，有关部门按体重偏瘦、正常、偏胖在这1000名学生中进行分层抽样，在等额抽取男生女生的前提下，已知抽取了16名体重偏胖的学生，试求在所有抽取的学生中男生人数；
（2）假设b≥150，c≥190，求这1000名学生中，体重偏胖的男生人数少于体重偏胖的女生人数的概率．

Answer 1

分析：（1）由题意可知，体重偏胖的学生人数为b+c=400，设1000名学生中应该抽取x人，则由

x

1000

=

16

400

，解得x的值，再根据所抽取的学生中男生与女生相等，可得所有抽取的学生中男生人数．
（2）由题意可得线性约束条件

150≤b≤210 190≤c≤250 b+c=400

，画出可行域，即图中直角三角形ABD及其内部区域．则本题即求c＜b的概率，而由几何概型可得c＜b的概率等于△BEM的面积除以直角三角形ABD的面积，计算求得结果．

解答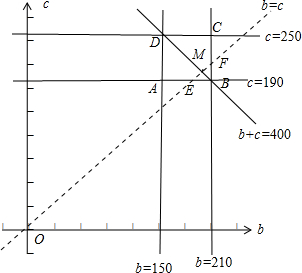：解：（1）由题意可知，体重偏胖的学生人数为b+c=400，设1000名学生中应该抽取x人，
则

x

1000

=

16

400

，解得x=40，又所抽取的学生中男生与女生相等，
故所有抽取的学生中男生人数为20人．
（2）由b+c=400，且b≥150，c≥190，可得线性约束条件

150≤b≤210 190≤c≤250 b+c=400

，
画出可行域，即图中直角三角形ABD及其内部区域．
则本题即求c＜b的概率．
如图所示：设直线c=b和AB、BC的交点分别为E、F，直线EF和BD的交点为M，
故c＜b的概率等于△BEM的面积除以直角三角形ABD的面积．
再由题意可得，直角三角形ABD的面积为

1

2

×60×60=1800，
点E（190，190 ）、F（210，210），M（200，200），
故△BEM的面积为

1

2

EB•（y_M-190）=

1

2

×20×10=100，
故c＜b的概率等于 

100

1800

=

1

18

．

点评：本题主要考查分层抽样的定义和方法，简单的线性规划，几何概型的应用，属于中档题．