题目内容
设双曲线 的右焦点为F2,过点F2的直线l与双曲线C相交于A,B两点,直线l的斜率为
的右焦点为F2,过点F2的直线l与双曲线C相交于A,B两点,直线l的斜率为 ,且
,且 ;
;(1)求双曲线C的离心率;
(2)如果F1为双曲线C的左焦点,且F1到l的距离为
 ,求双曲线C的方程.
,求双曲线C的方程.
【答案】分析:(1)利用双曲线的第二定义可求得双曲线C的离心率;
(2)利用点到直线间的距离公式可求得由F1到l的距离为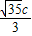 ,于是有
,于是有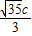 =
=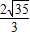 ,可求得c,继而可得a2,b2的值,从而可求得双曲线C的方程.
,可求得c,继而可得a2,b2的值,从而可求得双曲线C的方程.
解答:解:作双曲线的右准线L:x=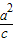 ,
,
分别作AA1⊥L,BB1⊥L,垂足分别为A1、B1,作BH⊥AA1,交AA1于H,
根据双曲线第二定义,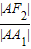 =
=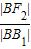 =e,(e是离心率),
=e,(e是离心率),
∵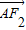 =2
=2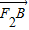 ,
,
∴|AA1|=2|BB1|=2|A1H|,
∴H为线段AA1的中点,故|A1H|=|AH|,
设|BB1|=m,则|AH|=m,|AA1|=2m①
∵直线AB的斜率为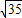 ,设AB与x轴成角为θ,则tanθ=
,设AB与x轴成角为θ,则tanθ=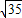 ,即
,即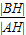 =
=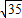 ,
,
∴|BH|=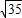 |AH|=
|AH|=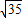 m,
m,
∴在直角三角形BHA中,|AB|=6m;
∴|AF2|=4m,②
由①②得:e=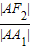 =
=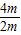 =2;
=2;
(2)∵直线方程l为:y=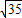 (x-c),即
(x-c),即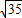 x-y-
x-y-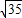 c=0,
c=0,
左焦点F1至AB距离d=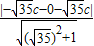 =
=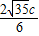 =
=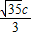 ,
,
又F1到l的距离为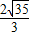 ,
,
∴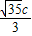 =
=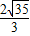 ,
,
∴c=2,又e=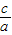 =2,
=2,
∴a=1,b=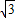 ,
,
∴双曲线方程为:x2-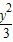 =1.
=1.
点评:本题考查双曲线的第二定义,考查点到直线间的距离公式,考查双曲线的性质的综合应用,属于难题.
(2)利用点到直线间的距离公式可求得由F1到l的距离为
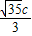 ,于是有
,于是有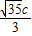 =
=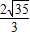 ,可求得c,继而可得a2,b2的值,从而可求得双曲线C的方程.
,可求得c,继而可得a2,b2的值,从而可求得双曲线C的方程.解答:解:作双曲线的右准线L:x=
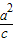 ,
,分别作AA1⊥L,BB1⊥L,垂足分别为A1、B1,作BH⊥AA1,交AA1于H,
根据双曲线第二定义,
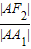 =
=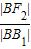 =e,(e是离心率),
=e,(e是离心率),∵
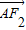 =2
=2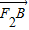 ,
,∴|AA1|=2|BB1|=2|A1H|,
∴H为线段AA1的中点,故|A1H|=|AH|,
设|BB1|=m,则|AH|=m,|AA1|=2m①
∵直线AB的斜率为
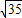 ,设AB与x轴成角为θ,则tanθ=
,设AB与x轴成角为θ,则tanθ=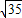 ,即
,即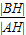 =
=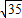 ,
,∴|BH|=
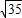 |AH|=
|AH|=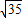 m,
m,∴在直角三角形BHA中,|AB|=6m;
∴|AF2|=4m,②
由①②得:e=
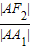 =
=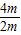 =2;
=2;(2)∵直线方程l为:y=
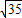 (x-c),即
(x-c),即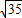 x-y-
x-y-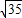 c=0,
c=0,左焦点F1至AB距离d=
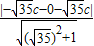 =
=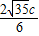 =
=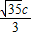 ,
,又F1到l的距离为
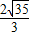 ,
,∴
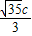 =
=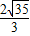 ,
,∴c=2,又e=
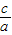 =2,
=2,∴a=1,b=
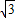 ,
,∴双曲线方程为:x2-
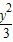 =1.
=1.点评:本题考查双曲线的第二定义,考查点到直线间的距离公式,考查双曲线的性质的综合应用,属于难题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为 的直线与双曲线的右支有且只有一个交点,则双曲线离心率的取值范围是
的直线与双曲线的右支有且只有一个交点,则双曲线离心率的取值范围是 的右焦点为F,右准线
的右焦点为F,右准线 与两条渐近线交于P,Q两点,如果
与两条渐近线交于P,Q两点,如果 是直角三角形,则双曲线的离心率为 (
)
是直角三角形,则双曲线的离心率为 (
) C.
C.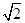 D.
D.
 的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A、B两点,与双曲线的其中一个交点为P,设O为坐标原点,若
的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A、B两点,与双曲线的其中一个交点为P,设O为坐标原点,若 ,且
,且 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )

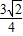

 的右焦点为F,右准线l与两条渐近线交于P,Q两点,如果△PQF是直角三角形,则双曲线的离心率为( )
的右焦点为F,右准线l与两条渐近线交于P,Q两点,如果△PQF是直角三角形,则双曲线的离心率为( )


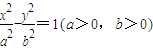 的右焦点为F(c,0),方程ax2+bx-c=0的两实根分别为x1,x2,则P(x1,x2)( )
的右焦点为F(c,0),方程ax2+bx-c=0的两实根分别为x1,x2,则P(x1,x2)( )