题目内容
11.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
| A. | $\frac{4}{3}$ cm3 | B. | $\frac{8}{3}$ cm3 | C. | 2cm3 | D. | 4cm3 |
分析 根据几何体的三视图知,该几何体是底面为正方形,
高为3的四棱锥,计算它的体积即可.
解答 解:根据几何体的三视图知,
该几何体是底面为正方形,高为3的四棱锥;
根据图中标出的尺寸,计算它的体积是
V=$\frac{1}{3}$×22×3=4(cm3).
故选:D.
点评 本题考查了利用空间几何体的三视图求体积的问题,是基础题.

练习册系列答案
相关题目
1.某几何体的三视图如图所示,则该几何体的体积为( )
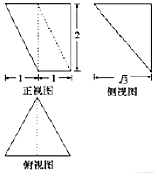

| A. | $\frac{11}{6}$$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
2.已知i是虚数单位,则(1+i)2的共轭复数是( )
| A. | -2i | B. | -2+i | C. | 2i | D. | 1+2i |
16.已知点P为不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.$所表示的平面区域内的一点,点Q是圆M:(x+1)2+y2=1上的一个动点,则|PQ|的最大值是( )
| A. | $\frac{{3\sqrt{5}+2}}{2}$ | B. | $\frac{{2\sqrt{5}+3}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $\sqrt{10}$ |
1.设$\overrightarrow{e_1}$,$\overrightarrow{e_2}$是不共线的向量,已知$\overrightarrow{AB}=\overrightarrow{e_1}+5\overrightarrow{e_2}$,$\overrightarrow{BC}=-2\overrightarrow{e_1}+8\overrightarrow{e_2}$,$\overrightarrow{CD}=3(\overrightarrow{e_1}-\overrightarrow{e_2})$,则( )
| A. | A、B、C三点共线 | B. | B、C、D三点共线 | C. | A、B、D三点共线 | D. | A、C、D三点共线 |
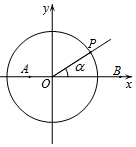 如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.
如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.