Question

如图1-4-4(a)中，CD垂直平分AB，点E在CD上，DF⊥AC，DG⊥BE，F、G分别为垂足.求证:AF·AC=BG·BE.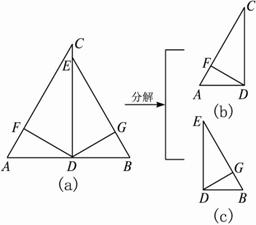

?

    图1-4-4

 

Answer 1

思路解析:将图1-4-4(a)分解出两个基本图形1-4-4(b)和(c)，再观察结论，就会发现，所要证的等积式的左、右两边分别满足图1-4-4(b)和(c)中的射影定理:AF·AC=AD²，BG·BE =DB²，通过代换线段的平方(AD²=DB²)就可以证明所要的结论.?

图1-4-4

证明:∵CD垂直平分AB，?

∴△ACD和△BDE均为直角三角形，并且AD =BD.?

又∵DF⊥AC，DG⊥BE，?

∴AF·AC =AD²，BG·BE =DB².?

∵AD²=DB²,?

∴AF·AC=BG·BE.