题目内容
已知 ,当x1、x2∈R且x1+x2=1时,总有
,当x1、x2∈R且x1+x2=1时,总有 .
.
(1)求m的值;
(2)设数列an满足 ,求an的通项公式.
,求an的通项公式.
解:(1)依题意,取 得
得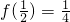 ,
,
即 ,所以m=2.
,所以m=2.
当m=2时,?x1、x2∈R,x1+x2=1,
有 ═
═ ,
,
所以m=2.
(2) ,
,
两式相加,并由已知得 ,
,
所以 .
.
分析:(1)根据题意,取,取 求得f(
求得f( )的值,进而根据函数解析式求得m的值.进而把m代入函数解析式求得f(x1)+f(x2)=
)的值,进而根据函数解析式求得m的值.进而把m代入函数解析式求得f(x1)+f(x2)= 恒成立,进而可知m的值.
恒成立,进而可知m的值.
(2) ,
, 两式,根据已知条件求得
两式,根据已知条件求得 ,进而求得an.
,进而求得an.
点评:本题主要考查了恒等、定值问题,倒序相加求数列通项,考查了学生综合运用所学知识的能力.
 得
得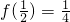 ,
,即
 ,所以m=2.
,所以m=2.当m=2时,?x1、x2∈R,x1+x2=1,
有
 ═
═ ,
,所以m=2.
(2)
 ,
,
两式相加,并由已知得
 ,
,所以
 .
.分析:(1)根据题意,取,取
 求得f(
求得f( )的值,进而根据函数解析式求得m的值.进而把m代入函数解析式求得f(x1)+f(x2)=
)的值,进而根据函数解析式求得m的值.进而把m代入函数解析式求得f(x1)+f(x2)= 恒成立,进而可知m的值.
恒成立,进而可知m的值.(2)
 ,
, 两式,根据已知条件求得
两式,根据已知条件求得 ,进而求得an.
,进而求得an.点评:本题主要考查了恒等、定值问题,倒序相加求数列通项,考查了学生综合运用所学知识的能力.

练习册系列答案
相关题目
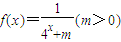 ,当x1、x2∈R且x1+x2=1时,总有
,当x1、x2∈R且x1+x2=1时,总有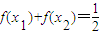 .
.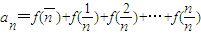 ,求an的通项公式.
,求an的通项公式.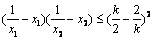 对任意(x1,x2) ∈D恒成立;
对任意(x1,x2) ∈D恒成立;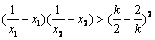 对任意(x1,x2) ∈D恒成立的k的范围.
对任意(x1,x2) ∈D恒成立的k的范围.
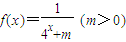 ,当x1、x2∈R且x1+x2=1时,总有
,当x1、x2∈R且x1+x2=1时,总有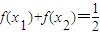 .
.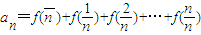 ,求{an}的通项公式;
,求{an}的通项公式;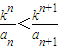 恒成立,求k的取值范围(其中k>0且k≠1).
恒成立,求k的取值范围(其中k>0且k≠1).