题目内容
已知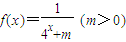 ,当x1、x2∈R且x1+x2=1时,总有
,当x1、x2∈R且x1+x2=1时,总有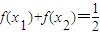 .
.(1)求m的值;
(2)设数列{an}满足
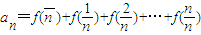 ,求{an}的通项公式;
,求{an}的通项公式;(3)对?n∈N*,
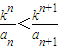 恒成立,求k的取值范围(其中k>0且k≠1).
恒成立,求k的取值范围(其中k>0且k≠1).
【答案】分析:(1)依据题意,取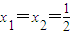 得
得 ,由此能求出m的值.
,由此能求出m的值.
(2)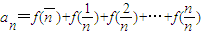 ,
,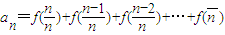 ,由此能够求出
,由此能够求出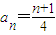 .
.
(3)由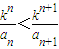 得
得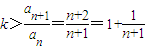 ,由此能够求出实数k的取值范围.
,由此能够求出实数k的取值范围.
解答:解:(1)依题意,取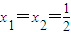 ,
,
得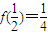 ,
,
即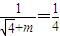 ,
,
所以m=2.
当m=2时,?x1、x2∈R,x1+x2=1,
有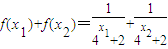 =
=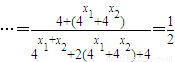 ,
,
所以m=2.
(2)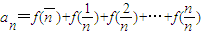 ,
,
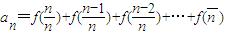
两式相加,并由已知得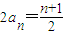 ,
,
所以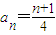 .
.
(3)由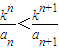 ,
,
得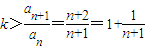 ,
,
?n∈N*,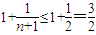 ,
,
等号当且仅当n=1时成立,
所以k的取值范围是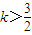 .
.
点评:本题考查数列与不等式的综合,其中:(1)是恒等、定值问题;(2)是根据(1)用倒序相加求数列通项;(3)是分离变量并求它的取值范围.对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.
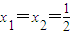 得
得 ,由此能求出m的值.
,由此能求出m的值.(2)
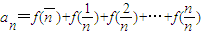 ,
,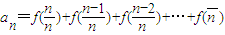 ,由此能够求出
,由此能够求出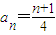 .
.(3)由
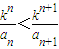 得
得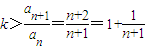 ,由此能够求出实数k的取值范围.
,由此能够求出实数k的取值范围.解答:解:(1)依题意,取
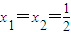 ,
,得
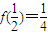 ,
,即
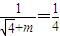 ,
,所以m=2.
当m=2时,?x1、x2∈R,x1+x2=1,
有
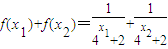 =
=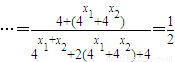 ,
,所以m=2.
(2)
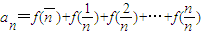 ,
,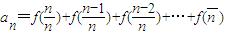
两式相加,并由已知得
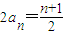 ,
,所以
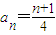 .
.(3)由
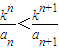 ,
,得
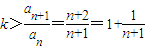 ,
,?n∈N*,
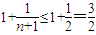 ,
,等号当且仅当n=1时成立,
所以k的取值范围是
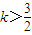 .
.点评:本题考查数列与不等式的综合,其中:(1)是恒等、定值问题;(2)是根据(1)用倒序相加求数列通项;(3)是分离变量并求它的取值范围.对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
相关题目
 ,当x1、x2∈R且x1+x2=1时,总有
,当x1、x2∈R且x1+x2=1时,总有 .
. ,求an的通项公式.
,求an的通项公式.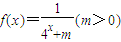 ,当x1、x2∈R且x1+x2=1时,总有
,当x1、x2∈R且x1+x2=1时,总有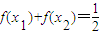 .
.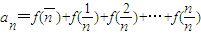 ,求an的通项公式.
,求an的通项公式.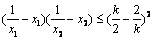 对任意(x1,x2) ∈D恒成立;
对任意(x1,x2) ∈D恒成立;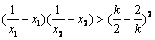 对任意(x1,x2) ∈D恒成立的k的范围.
对任意(x1,x2) ∈D恒成立的k的范围.