题目内容
设等差数列{an}的前n项和为Sn,且S4=－62,S6=－75.求:(1){an}的通项公式an及Sn;
(2)|a1|+|a2|+|a3|+…+|a14|.
解:(1)由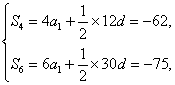
解得
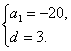
∴an=－20+(n－1)×3=3n－23,
Sn=
n2－
n.
(2)原式=(|－20|+|－17|+…+|－2|)+(1+4+7+…+19)
=
+
=147.
练习册系列答案
相关题目
题目内容
设等差数列{an}的前n项和为Sn,且S4=－62,S6=－75.求:(1){an}的通项公式an及Sn;
(2)|a1|+|a2|+|a3|+…+|a14|.
解:(1)由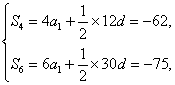解得
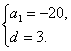
∴an=－20+(n－1)×3=3n－23,
Sn=n2－n.
(2)原式=(|－20|+|－17|+…+|－2|)+(1+4+7+…+19)
=+=147.