题目内容
证明函数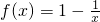
在（-∞，0）上是增函数．
解：任取x1，x2∈（-∞，0），且x1＜x2，
则f（x1）-f（x2）=（1-
）-（1-
）=
，
因为x1＜x2＜0，所以x1-x2＜0，x1x2＞0，
所以f（x1）-f（x2）＜0，即f（x1）＜f（x2）．
所以函数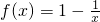在（-∞，0）上是增函数．
分析：任取x1，x2∈（-∞，0），且x1＜x2，通过作差比较f（x1）与f（x2）的大小，根据增函数的定义可得结论．
点评：本题考查函数单调性的证明，对于单调性的证明一般有两种方法：一是定义；一是导数．
则f（x1）-f（x2）=（1-
）-（1-）=，因为x1＜x2＜0，所以x1-x2＜0，x1x2＞0，
所以f（x1）-f（x2）＜0，即f（x1）＜f（x2）．
所以函数
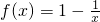在（-∞，0）上是增函数．分析：任取x1，x2∈（-∞，0），且x1＜x2，通过作差比较f（x1）与f（x2）的大小，根据增函数的定义可得结论．
点评：本题考查函数单调性的证明，对于单调性的证明一般有两种方法：一是定义；一是导数．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
附加题：
在(－¥
，0)上是减函数．
在(－¥
，0)上是减函数．
在（－∞，0）上是增函数。