题目内容
设![]()
![]() 。
。
(1)若![]() 是函数
是函数![]() 的极大值点,求
的极大值点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若在
时,若在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
(1)![]()
(2)![]()
解析:
![]()
(2分)
当![]() 时,
时,

当![]() 时,
时,

当![]() 时,
时,

当![]() 时,
时,

综上所述,当![]() ,即
,即![]() 时,
时,![]() 是函数
是函数![]() 的极大值点. (7分)
的极大值点. (7分)
(2)在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,等价于
成立,等价于
当![]() 时,
时, ![]() . (9分)
. (9分)
由(1)知,①当![]() ,即
,即![]() 时,
时,
函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
![]() .
.
由![]() ,解得
,解得![]() .
.
由![]() ,解得
,解得![]()
![]() ,
, ![]() ; (12分)
; (12分)
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]() .
.
综上所述,当![]() 时,在
时,在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立. (14分)
成立. (14分)

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
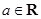 ,函数
,函数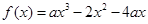 ,
, 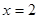 是函数
是函数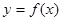 的极值点,求
的极值点,求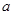 的值;
的值;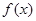 在区间
在区间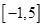 上的最值.
上的最值.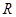 上为单调函数,若是,求出
上为单调函数,若是,求出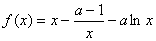
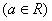 .
.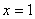 是函数
是函数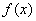 的极大值点,求
的极大值点,求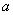 的取值范围;
的取值范围;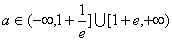 时,若在
时,若在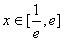 上至少存在一点
上至少存在一点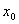 ,使
,使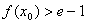 成立,求
成立,求