题目内容
设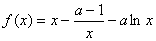
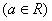 .
.
(1)若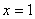 是函数
是函数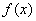 的极大值点,求
的极大值点,求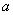 的取值范围;
的取值范围;
(2)当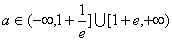 时,若在
时,若在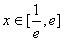 上至少存在一点
上至少存在一点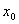 ,使
,使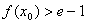 成立,求
成立,求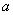 的取值范围.
的取值范围.
【答案】

(2分)
|
|
|
|
|
|
|
|
|
|
|
|
递减 |
极小值 |
递增 |
当 时,
时,
当 时,
时,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
极大值 |
递减 |
极小值 |
递增 |
当 时,
时,
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
非极值 |
递增 |
当 时,
时,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
极大值 |
递减 |
极小值 |
递增 |
综上所述,当 ,即
,即 时,
时, 是函数
是函数 的极大值点.
(7分)
的极大值点.
(7分)
(2)在 上至少存在一点
上至少存在一点 ,使
,使 成立,等价于
成立,等价于
当 时,
时,  .
(9分)
.
(9分)
由(1)知,①当 ,即
,即 时,
时,
函数 在
在 上递减,在
上递减,在 上递增,
上递增,
 .
.
由 ,解得
,解得 .
.
由 ,解得
,解得
 ,
,  ; (12分)
; (12分)
②当 ,即
,即 时,函数
时,函数 在
在 上递增,在
上递增,在 上递减,
上递减,
 .
.
综上所述,当 时,在
时,在 上至少存在一点
上至少存在一点 ,使
,使 成立.
(14分)
成立.
(14分)

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目












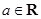 ,函数
,函数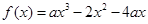 ,
, 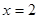 是函数
是函数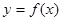 的极值点,求
的极值点,求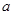 的值;
的值;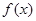 在区间
在区间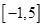 上的最值.
上的最值.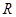 上为单调函数,若是,求出
上为单调函数,若是,求出