题目内容
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:

(Ⅰ)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(Ⅱ)以上述样本的频率作为概率,从该校高三学生中有放回地抽取3人,记抽取的学生成绩不低于90分的人数为 ,求
,求 的分布列和期望.
的分布列和期望.
(Ⅰ)92分;(Ⅱ)分布列详见解析, .
.
【解析】
试题分析:本题主要考查频率分布直方图的读图能力和计算能力,以及离散型随机变量的分布列与数学期望.第一问根据频率分布直方图,求该校高三学生本次数学考试的平均分,解决实际问题,公式为:每一个区间的中点×每一个长方形的高×组距,把所得结果相加即可;第二问利用频率=高×组距,求出样本中成绩不低于90分的频率,通过分析发现人数 符合二项分布,利用二项分布的概率计算公式:
符合二项分布,利用二项分布的概率计算公式: 来计算每种情况的概率,列出分布列,由于
来计算每种情况的概率,列出分布列,由于 ,所以利用上面的公式计算期望.
,所以利用上面的公式计算期望.
试题解析:(Ⅰ)由频率分布直方图,得该校高三学生本次数学考试的平均分为
 5分
5分
(Ⅱ)样本中成绩不低于90分的频率为
 ,
,
所以从该校高三学生中随机抽取1人,分数不低于90分的概率为 . 7分
. 7分
由题意, ,
, (
( ),
),
其概率分布列为:
|
X |
0 |
1 |
2 |
3 |
|
P |
0.064 |
0.288 |
0.432 |
0.216 |
10分
 的期望为
的期望为
 .
.
考点:1.频率分布直方图;2.分布列;3.数学期望.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案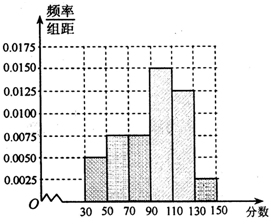 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图: 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下: 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:根据频率分布直方图,估计该校高三学生本次数学考试的平均分
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:根据频率分布直方图,估计该校高三学生本次数学考试的平均分
 和
和
 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在