题目内容
 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:(Ⅰ)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(Ⅱ)以上述样本的频率作为概率,从该校高三学生中有放回地抽取3人,记抽到的学生成绩不低于90分的人数为X;求X的分布列和期望.
分析:(Ⅰ)由题意及频率分布直方图及平均数的定义即可求估计本次考试的平均分;
(Ⅱ)抽到的学生成绩不低于90分的人数X的取值可能为0,1,2,3,然后求出每个学生成绩低于90分的概率和不低于90分的概率,再分别求出X=0,1,2,3时的概率,列出分布列,最后利用数学期望的公式解之即可.
(Ⅱ)抽到的学生成绩不低于90分的人数X的取值可能为0,1,2,3,然后求出每个学生成绩低于90分的概率和不低于90分的概率,再分别求出X=0,1,2,3时的概率,列出分布列,最后利用数学期望的公式解之即可.
解答:解:(Ⅰ)由频率分布直方图,得该校高三学生本次数学考试的平均分为平均分为:
=40×0.1+60×0.15+80×0.15+100×0.3+120×0.25+140×0.05=92.
(Ⅱ)抽到的学生成绩不低于90分的人数X的取值可能为0,1,2,3
因为以上述样本的频率作为概率
所以每个学生成绩低于90分的概率为(0.005+0.0075+0.0075)×20=
,不低于90分的概率为
P(X=0)=(
)3=
,P(X=1)=
(
)1(
)2=
,P(X=2)=
(
)2(
)1=
,P(X=3)=(
)3=
分布列如下
∴E(X)=0×
+1×
+2×
+3×
=
∴X的期望为
. |
| x |
(Ⅱ)抽到的学生成绩不低于90分的人数X的取值可能为0,1,2,3
因为以上述样本的频率作为概率
所以每个学生成绩低于90分的概率为(0.005+0.0075+0.0075)×20=
| 2 |
| 5 |
| 3 |
| 5 |
P(X=0)=(
| 2 |
| 5 |
| 8 |
| 125 |
| C | 1 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 36 |
| 125 |
| C | 2 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 54 |
| 125 |
| 3 |
| 5 |
| 27 |
| 125 |
分布列如下
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 8 |
| 125 |
| 36 |
| 125 |
| 54 |
| 125 |
| 27 |
| 125 |
| 9 |
| 5 |
∴X的期望为
| 9 |
| 5 |
点评:本题考查频率分布直方图的应用,概率的求法,离散型随机变量的期望与方差,考查分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目
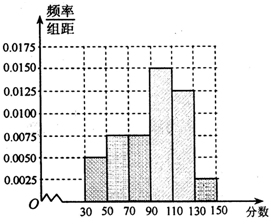 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图: 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:根据频率分布直方图,估计该校高三学生本次数学考试的平均分
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:根据频率分布直方图,估计该校高三学生本次数学考试的平均分
 ,求
,求
 和
和
 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在