题目内容
函数f(x)= 若方程f(x)=x+a有且只有两个不等的实数根,则实数a的取值范围为
若方程f(x)=x+a有且只有两个不等的实数根,则实数a的取值范围为
| A.(-∞,0) | B.[0,1) | C.(-∞,1) | D.[0,+∞) |
C
解析试题分析:根据题意从而得到
函数f(x)= 的图象如图所示,
的图象如图所示,
当a<1时,函数y=f(x)的图象与函数y=x+a的图象有两个交点,
即方程f(x)=x+a有且只有两个不相等的实数根
故选:C
考点:本题考查的知识点是根的存在性及根的个数的判断.
点评:解决方程根的问题,一般来说,可以直接法求解方程,也可以采用分离为两个函数对应相等,利用图像的交点情况来说明。将方程f(x)=x+a根的个数,转化为求函数零点的个数,并用图象法进行解答是本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
设函数 若
若 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
函数 在区间
在区间 上单调递减,那么实数
上单调递减,那么实数 的取值范围是( )
的取值范围是( )
A. ≤-2 ≤-2 | B. ≥-2 ≥-2 | C. ≤4 ≤4 | D. ≥4 ≥4 |
大西洋鲑鱼每年都要逆流而上游回产地产卵.经研究发现:鲑鱼的游速v(单位:m/s)与耗氧量的单位数 的函数关系式为:
的函数关系式为: 。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=
。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=
| A.9 | B.8 | C.3 | D.2 |
如果二次函数 有两个不同的零点,则
有两个不同的零点,则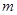 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
函数f(x)=lnx- 的零点一定位于区间( )
的零点一定位于区间( )
A.( ,1) ,1) | B.(1,2) | C.(2,e) | D.(e,3) |
函数 的增区间是( )
的增区间是( )
A.( ,2] ,2] | B.[2,  ) ) | C.( ,3] ,3] | D.[3,  ) ) |
已知函数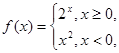 则
则 ( )
( )
| A.16 | B. | C.4 | D.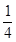 |
 与指数函数
与指数函数 在同一坐标系中的图象可能是
在同一坐标系中的图象可能是