题目内容
函数 在区间
在区间 上单调递减,那么实数
上单调递减,那么实数 的取值范围是( )
的取值范围是( )
A. ≤-2 ≤-2 | B. ≥-2 ≥-2 | C. ≤4 ≤4 | D. ≥4 ≥4 |
A
解析试题分析:因为 图象开口向上,所以为使其在区间
图象开口向上,所以为使其在区间 上单调递减,须对称轴x=
上单调递减,须对称轴x=
 3,解得
3,解得 ≤-2,故选A。
≤-2,故选A。
考点:本题主要考查二次函数的图象和性质。
点评:典型题,研究二次函数的单调性,要看图象的开口方向,看对称轴位置。

练习册系列答案
相关题目
已知幂函数 的图像经过点
的图像经过点 ,则
,则 的值等于
的值等于
| A.16 | B. | C.2 | D. |
设 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
北京时间2012年10月11日19点,瑞典文学院诺贝尔奖评审委员会宣布,中国作家莫言获得2012年诺贝尔文学奖,全国反响强烈,在全国掀起了出书的热潮.国家对出书所得稿费纳税作如下规定:不超过800元的不纳税;超过800元而不超过4000元的按超过部分的14%纳税;超过4000元的按全稿酬的11%纳税.某人出版了一书共纳税420元,这个人的稿费为
| A.3000元 | B.3800元 | C.3818元 | D.5600元 |
函数 的图象与直线
的图象与直线 的图象有一个公共点,则实数
的图象有一个公共点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. 或 或 | D. |
对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值1叫做
的最小值1叫做 的上确界,若
的上确界,若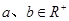 ,且
,且 ,则
,则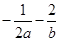 的上确界为( )
的上确界为( )
A. | B. | C. | D.-4 |
函数f(x)= 若方程f(x)=x+a有且只有两个不等的实数根,则实数a的取值范围为
若方程f(x)=x+a有且只有两个不等的实数根,则实数a的取值范围为
| A.(-∞,0) | B.[0,1) | C.(-∞,1) | D.[0,+∞) |

 的零点个数为
的零点个数为
| A.3 | B.2 | C.1 | D.0 |
 满足:对任意x∈R,都有
满足:对任意x∈R,都有 成立,且当
成立,且当 时,
时, (其中
(其中 为
为 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )


