题目内容
袋中装有4个白球,2个黑球,从袋中一次任意取出2个球,求下列事件发生的概率;
(Ⅰ)事件A:取出的2个球均为白球;
(Ⅱ)事件B:取出的2个球颜色不相同.
(Ⅰ)事件A:取出的2个球均为白球;
(Ⅱ)事件B:取出的2个球颜色不相同.
分析:(1)用用列举法可得从袋中6个球中一次任意取出2个球的基本事件的个数为
,其中取出的2个球均为白球的个数为
,再利用古典概型的概率计算公式即可得出;
(2)取出的2个球颜色不相同包括
个基本事件,再利用古典概型的概率计算公式即可得出.
| C | 2 6 |
| C | 2 4 |
(2)取出的2个球颜色不相同包括
| C | 1 4 |
| C | 1 2 |
解答:解:设4个白球的编号为1,2,3,4,2个红球的编号为a,b,从袋中的6个球中任取2个球的方法有:(1,2),(1,3),(1,4),(1,a),(1,b),(2,3),(2,4),(2,a),(2,b),(3,4),(3,a),(3,b)(4,a),(4,b),(a,b)共15种情况.
(1)从袋中的6个球中任意取出2个,2个都是白球的取法有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种情况,
所以取出的2球全是白球的概率P(A)=
=
.
(2)从袋中的6个球中任意取出2个,2个球颜色不同的取法有(1,a),(1,b)(2,a),(2,b),(3,a),(3,b),(4,a),(4,b)共8种情况,
所以取出的2个球颜色不相同的概率P(B)=
.
(1)从袋中的6个球中任意取出2个,2个都是白球的取法有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种情况,
所以取出的2球全是白球的概率P(A)=
| 6 |
| 15 |
| 2 |
| 5 |
(2)从袋中的6个球中任意取出2个,2个球颜色不同的取法有(1,a),(1,b)(2,a),(2,b),(3,a),(3,b),(4,a),(4,b)共8种情况,
所以取出的2个球颜色不相同的概率P(B)=
| 8 |
| 15 |
点评:本题考查了古典概型的概率计算方法,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
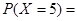 ___________.
___________.