题目内容
一袋中装有4个白球,2个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现3次停止,则P(X=5)= .(X表示次数)
分析:由题意可得,每次取到红球的概率都是
,前四次取到了2个红球,第五次取得红球,再根据互独立事件的概率乘法公式可得P(X=5)=
•(
)2•(
)2•
,
计算求得结果.
| 2 |
| 6 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
计算求得结果.
解答:解:由题意可得,每次取到红球的概率都是
=
,
X=5表示前四次取到了2个红球,第五次取得红球,
故P(X=5)=
•(
)2•(
)2•
=
,
故答案为:
.
| 2 |
| 6 |
| 1 |
| 3 |
X=5表示前四次取到了2个红球,第五次取得红球,
故P(X=5)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
故答案为:
| 8 |
| 81 |
点评:本题主要考查相互独立事件的概率乘法公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
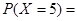 ___________.
___________.